<论文拾萃>基于近似动态规划方法的时变需求地铁节能调度设计

2022-11-15

本论文于2020年发表于交通领域知名期刊 IEEE TRANSACTIONS ON SYSTEMS 上。本文解决一种具有时间依赖需求的节能地铁列车调度问题，提出了一种列车交通模型，建立了基于列车车头时距、列车载客量和地铁沿线能耗演化的动态方程。为了克服优化问题中的维度灾难问题，本文构建了一个近似动态规划（ADP）框架，引入了状态、策略、状态转换和奖励函数的概念。通过数值实验验证了所提模型和算法的有效性，并与遗传算法和差分进化算法进行了比较，证明该算法能够在较短的时间内收敛到一个较好的解。

问题场景

本文在所研究的城市轨道交通系统上做出以下假设：

  • 关注一个单方向的轨道交通线，地铁可以在任一站停止
  • 所有地铁均从起始站出发，以先进先出的方式运行
  • 乘客上车速度是无上界的，因此地铁在某站的停留时间不受该站人数的影响

地铁运行路线图

而本文的目标是：制定一个较优的地铁时刻表，在考虑乘客流的情况下实现地铁利用率最大化，乘客舒适水平较优以及能源消耗相对较少

问题建模

  • 决策变量：
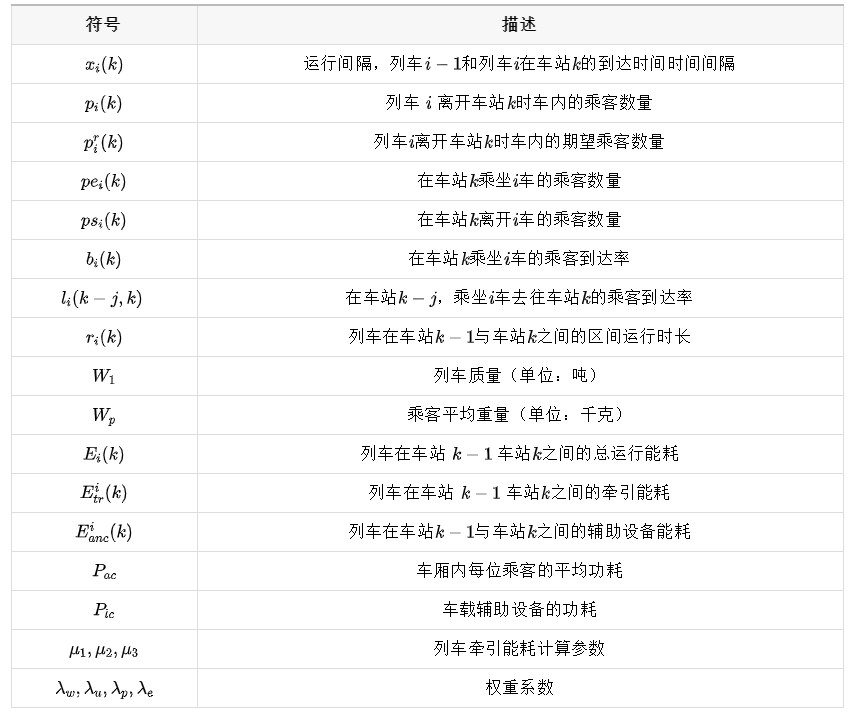
决策变量 描述
$x_i(l)$ 运行间隔，$i-1$车与 $i$ 车在始发站的到达时间间隔
$s_i(k)$ $i$ 车在车站 $k$ 的停站时长

image-20221115190934130.png

  • 目标函数：
    • 顾客在车站的平均等待时间：旨在提高列车运行效率
    • 发车数量：控制运营成本
    • 实际列车载客量与期望列车载客量的偏差：提高乘客舒适度
    • 列车在运行中的能耗：降低能耗

  • 约束条件：

    • 状态转移方程：$x_i(k+1) = x_i(k) + s_i(k) - s_{i-1}(k)$

      $i-1$车与 $i$ 车在 $k+1$ 站的到达时间间隔 = $i-1$车与 $i$ 车在 $k$ 站的到达时间间隔 + 两车在 $k$ 站的停车时长之差

    • 状态转移方程：$p_i(k) = p_i(k-1) + b_i(k)[x_i(k)+s_i(k)-s_{i-1}(k)]$

      $i$ 车离开 $k$ 站时车内乘客数量 = 离开$k-1$站时车内乘客数量 + 在车站 $k$ 的乘客到达率 * 与上一车的到达时间间隔 - 在车站 $k$ 下车的人数

    • 能耗方程

    • 决策变量边界约束

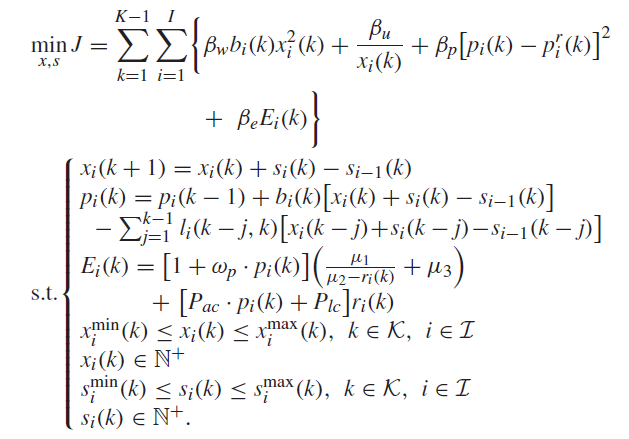
image-20221115192308786.png

算法设计

ADP框架：决策者被称为“智能体”，智能体之外所有与它产生交互的事物称为环境或者解空间。一旦智能体选择了动作，环境将对那些动作做出反应并完成一次更新。同时，环境会产生奖励，而这一奖励将随着迭代由智能体最小化(或最大化)。换言之，智能体与环境在每次迭代产生交互。智能体首先接受环境的状态信息(即 $S_t$ )并相应地选择动作 $a_t$ 。然后，作为此次选择动作的结果，智能体将接收到奖励，即 $R(s_t, a_t)$ 并将环境转换至新的状态 $s_{t+1}$

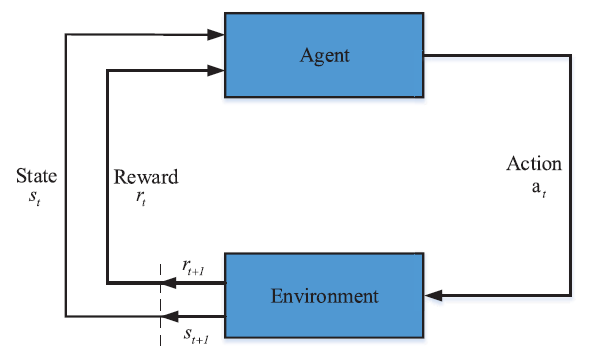
image-20221115193235461.png

ADP的基本元素

符号 定义
$S_i(k)$ 列车 $i$ 到达车站 $k$ 时的状态变量
$a_i(k)$ 列车 $i$ 在车站 $k$ 选择的动作
$R(S_i(k),a_i(k))$ 当列车 $i$ 处于状态 $S_i(k)$ 时采用动作 $a_i(k)$ 的奖励函数
$\gamma$ 消减函数
$S$ 所有可能状态变量的集合
$A$ 每列车所有可能采取的动作的集合

求解算法

采取向前策略：通过求解所有列车在各个决策阶段的一个近似问题以做出决策

通过求解以下优化问题做出最优策略：

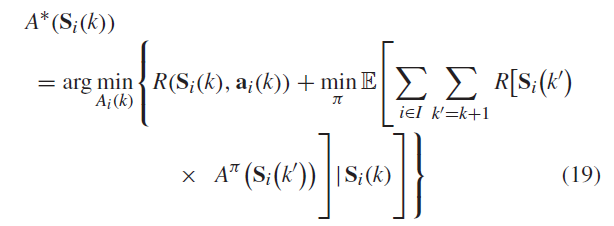
image-20221115193351509.png

image-20221115193555281.png

ADP中的近似函数

ADP的关键在于近似函数的确定。

通常ADP中的近似函数可分为三种基本类别：

  • 查表法：确定每种状态 $S_t$ 选择动作 $a_t$ 后的 $V$，通过查表法精确获得
  • 参数模型：建立模型对近似函数进行精确求解
  • 非参数模型：利用启发式算法进行估计

算例试验

  • 比较相同算例下ADP与GA、DEA的目标函数值与计算时间，发现ADP计算时间远远小于GA，但解的质量要逊于GA、DEA
  • 比较不同权重系数的影响

参考文献：

Liu R, Li S, Yang L, et al. Energy-efficient subway train scheduling design with time-dependent demand based on an approximate dynamic programming approach[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2018, 50(7): 2475-2490.