本文于2020年上传于Arxiv上。在传统rollout算法的基础上,作者将其应用延伸到受约束的确定性动态规划,包括组合优化问题。在合适的假设下,作者证明了如果基础的启发式算法能够提供可行解,则rollout算法有一个很好的质量改善性质:它能够产生一个可行解,质量不差于基础启发式算法的解的质量。
除此外,作者还关注了multiagent问题,在该问题中每个阶段由多个组分组成,每个由一个agent负责,通过成本函数、约束或两者进行耦合。我们可以通过来一个可选项的实现来极大降低计算需求,实现多agent问题中rollout的使用,做到质量改善。
1. Introduction
考虑确定性最优控制问题:
\[x_{k+1}=f_k(x_k,u_k), \quad k=0,...,N-1\]$x_k$ 为state,$u_k$ 为时刻 $k$ 时的control,$f_k$ 为函数,初始状态为 $x_0$
Complete trajectory : $T = (x_0,u_0,x_1,u_1,…,u_{N-1},x_N) $
partial trajectory : Complete trajectory 的子集,由时间连续的状态和控制组成
因此,我们的问题为:
\[\min_{T \in C}G(T)\]$G$ 为给定的实值成本函数,$C$ 为给定的 trajectory 约束集合
通常情况下,
\[G(x_0,u_0,x_1,u_1,...,u_{N-1},x_N) = g_N(x_N)+\sum_{k=0}^{N-1}g_k(x_k,u_k)\]$g_k, k=0,1,…,N$ 为给定的实值函数,并且control均满足与时间不关联的约束:
\[u_k \in U_k(x_k), \quad k=0,1,...,N-1\]这是标准问题规划,通常作为DP的起点。而我们的目标在于解决带有更复杂约束的问题,其中精确解是很难得到的。
rollout 算法的总体思想是从一个次优解算法(base heurstic)出发,并以成本改进作为目标:保证(在适当的假设下)rollout算法能够产生一个可行解,其成本不低于基础启发式对应的成本。
受约束的DP问题可以转化为无约束DP问题。思路是重新定义 stage $k$ 下的state为 partial trajectory :
\[y_k = (x_0,u_0,x_1,...,u_{k-1},x_k)\]state 按照下列等式变化:
\[y_{k+1} = (y_k,u_k,f_k(x_k,u_k))\]因此,问题转化为寻找最小化最终成本 $G(y_N)$ 的序列,满足 $y_N \in C$
但按照以上的公式,求解问题的精确解通常是不切实际的,因为相关的计算量过于庞大。
Using a Base Heuristic for Constrained Rollout
我们假定 base heuristic 是可行的,即对于任意给定的 partial trajectory $y_k=(x_0,u_0,x_1,…,u_{k-1},x_k)$ 可以产生一个 (complementary) partial trajactory $R(y_k) = (x_k,u_k,x_{k+1},u_{k+1},…,u_{N-1},x_N)$
该 partial trajactory 从 $x_k$ 出发,且满足 $x_{t+1}=f_t(x_t,u_t), t = k,…,N-1$
因此,给定 $y_k$ 和 任一control $u_k$ 后,我们可以如下利用 base heuristic 来得到一条 complete trajactory:
- 生成下一个state $x_{k+1} = f_k(x_k,u_k)$
- 扩展 $y_{k+1}=(y_k,u_k,f_k(x_k,u_k))$
- 从 $y_{k+1}$ 出发运行 base heuristic 得到 $R(y_{k+1})$
- 连接 $y_{k+1}$ 与 $R(y_{k+1})$ 得到 complete trajectory $T_k(y_k,u_k) = (y_k,u_k,R(y_{k+1}))$
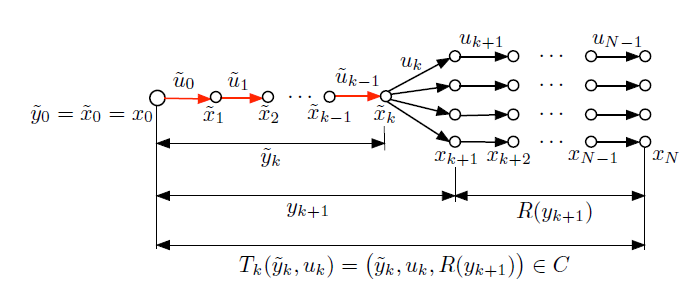
显然,$T_k(y_k,u_k) = (y_k,u_k,R(y_{k+1}))$ 只在 $u_k$ 的一个子集内可行:
\[U_k(y_k)=\left \{ u_k| T_k(y_k,u_k) \in C\right \}\]而 rollout 算法从给定初始状态 $\tilde{y}_0 = \tilde{x}_0$出发,产生后续的 partial trajectories $\tilde{y}_1, …,\tilde{y}_N$ 满足:
\(\tilde{y}_{k+1}=(\tilde{y}_k,\tilde{u}_k,f_k(\tilde{x}_k,\tilde{u}_k)),\quad k=0,1,...,N-1\) $\tilde{x}_k$ 是 $\tilde{y}_k$ 最后一个状态分量,$\tilde{u}_k$ 是在 $T_k(\tilde{y}_k,u_k)$ 可行域上最小化启发式函数成本 $H(T_k(\tilde{y}_k,u_k))$ 的control。
在stage $k$,算法得到集合 $U_k(\tilde{y}_k)$ 并且从 $U_k(\tilde{y}_k)$ 中选取 $\tilde{u}_k$ 最小化 complete trajectory $T_k(\tilde{y}_k,u_k)$ 的成本 :
\[\tilde{u}_k \in arg \min_{u_k \in U_k(\tilde{y}_k)} G(T_k(\tilde{y}_k,u_k))\]目标是产生一个可行的最终 complete trajectory $\tilde{y}_k$ ,其成本为 $G(\tilde{y}_N)$ 不大于 $R(\tilde{y}_0)$ 的成本($R(\tilde{y}_0)$ 为base heuristic从$\tilde{y}_0$开始所产生的序列)。
\[G(\tilde{y}_N) \leq G(R(\tilde{y}_0))\]2. Cost Improvement with the Rollout Algorithm
接下来,我们将会介绍能够保证 $U_k(\tilde{y}_k)$ 非空的条件,并且 complete trajectories $T_k(\tilde{y}_k, \tilde{u}_k)$ 的成本随着 $k$ 而改善:
\[G(T_{k+1}(\tilde{y}_{k+1},\tilde{u}_{k+1}))\leq G(T_k(\tilde{y}_k,\tilde{u}_k)),\quad k=0,1,...,N-1\]在第一步有:
\[G(T_{0}(\tilde{y}_{0},\tilde{u}_{0}))\leq G(R(\tilde{y}_0))\]Def 2.1: We say that the base heuristic is sequentially consistent if whenever it generates a partial trajectory
\[(x_k,u_k,x_{k+1},...,u_{N-1},x_N)\]starting from a partial trajectory $y_k$, it also generates the partial trajectory
\[(x_{k+1},u_{k+1},...,u_{N-1},x_N)\]starting from the partial trajectory $y_{k+1}=(y_k,u_k,x_{k+1})$
比如说,贪心算法就是 sequentially consistent 的。DP问题中旨在最小化最终成本 $G(y_N)$ 的任何策略(一个反馈控制函数 $\mu_k(y_k),k=0,1,…,N-1$),依照系统等式 $y_{k+1} = (y_k,u_k,f_k(x_k,u_k))$ 与可行性约束 $y_N \in C$ 都可以视为是 sequentially consistent的
对于给定的 partial trajectory $y_k$ ,让我们定义 $y_k \cup R(y_k)$ 为通过连接 $y_k$ 和 base heuristic 从 $y_k$ 开始生成的 partial trajectory 连接而成的 complete trajectory。因此,若 $y_k = (x_0,u_0,…,u_{k-1}, x_k)$ 且 $R(y_k) = (x_k,u_{k+1},…,u_{N-1},u_N)$,则我们可以得到:
\[y_k \cup R(y_k) =(x_0,u_0,...,u_{k-1}, x_k,u_{k+1},...,u_{N-1},u_N)\]Def 2.2 : We say that the base heuristic is sequentially improving if for every $k$ and partial trajectory $y_k$ for which $y_k \cup R(y_k) \in C$, the set $U_k(y_k)$ is nonempty, and we have
\[G(y_k \cup R(y_k)) \geq \min_{u_k \in U_k(y_k)} G(T_k(y_k,u_k))\]
| 注意到,如果 base heuristic 是 sequentially consistent 的,则它也是 sequentially improving 的。因为对于一个 sequentially consistent 的 heuristic 而言,它所生成的 $y_k \cup R(y_k)$ 等于 集合 ${T_k(y_k,u_k) | u_k \in U_k(y_k)}$ 中的一个元素。 |
而本文的主要结论如下所示:
Proposition 2.1: Assume that the base heuristic is sequentially improving and generates a feasible complete trajectory starting from the initial state $\tilde{y}_0 = \tilde{x}_0$, i.e., $R(\tilde{y}_0) \in C$. Then for each $k$, the set $U_k(\tilde{y}_k)$ is nonempty, and we have
\[G(R(\tilde{y}_0))\geq G(T_0(\tilde{y}_0,\tilde{u}_0))\geq G(T_1(\tilde{y}_1,\tilde{u}_1)) \geq ...\geq G(T_{N-1}(\tilde{y}_{N-1},\tilde{u}_{N-1})) = G(\tilde{y}_N)\]where $T_k(\tilde{y}_k,\tilde{u}_k) = (\tilde{y}_k,\tilde{u}_k,R(\tilde{y}_k + 1))$. In particular, the final trajectory $\tilde{y}_N$ generated by the constrained rollour algorithm is feasible and has no larger cost than the trajectory $R(\tilde{y}_0) $ generated by the base heuristic starting from the inital state.

Proof.
考虑 $R(\tilde{y}_0)$,base heuristic 生成的由 $\tilde{y}_0 $ 出发的 complete trajectory。
因为 $\tilde{y}_0 \cup R(\tilde{y}_0) = R(\tilde{y}_0) \in C$,所以根据 sequential improvement 的性质有:
\(G(R(\tilde{y}_0)) \geq G(T_0(\tilde{y}_0,\tilde{u}_0))\) $R(\tilde{y}0) = (\tilde{x}_0,u{1},…,u_{N-1},u_N)$
$T_0(\tilde{y}0,\tilde{u}_0)=(\tilde{y}_0,\tilde{u}_0,R(\tilde{y}_1)) = (\tilde{x}_0,\tilde{u}_0,x_1,…,u{k-1},x_k)$
