本论文于2018年发表于交通领域知名期刊 Transportation Science 上。本文在队列网络中引入了一个随机定向的问题,旅行者必须在每个节点的时间窗口内到达并进入服务以收集奖励,但旅行者可能在服务开始之前在每个地点经历随机的等待时间。为了最大限度地获得预期奖励,旅行者必须决定去哪些地方,以及在每个地方排队多长时间。本文将该问题建模为一个马尔可夫决策过程,目标是最大化预期收集的奖励。为了解决这一问题,本文提出了一种基于rollout算法的近似动态规划方法。该方法引入了一个两阶段的启发式估计,我们称之为compound rollout。在第一阶段,算法决定是留在当前位置还是去另一个位置。如果离开当前位置,则在第二阶段选择下一个位置。通过将动态策略与具有追索权操作的优先路由解决方案进行比较,本文展示了建模和解决方案的价值。
1.1 问题描述
在定向问题中,一个旅行者需要决定参观一个目的地子集的路径,在每个参观的地点收集奖励来最大化在特定时间范围内得到的总奖励。在本研究中,我们在定向问题中引入了一个变量:旅行者在他参观的地点处可能会经历排队等待。为了收集该地点的奖励,旅行者必须在队列中等待,并且在该地点时间窗结束前会见顾客。在旅行者到达地点前,他并不知道队列的长度,并且等待时间是随机的。
每个地点的队列由旅行者的竞争对手组成。由于竞争对手的到达时间、离开时间、服务时间不确定,因此旅行者在队列中的等待时间是不确定的。给定一个地点列表,旅行者需要确定参观的地点和参观的顺序来最大化期望奖励。一旦到达某个地点,旅行者需要决定是否要加入队列等待或是立即离开前往下一个地点。只有在该地点的预定时间窗内进入服务,旅行者才可以收集到该地点的奖励。我们称该问题为带有排队和时间窗的动态定向问题(dynamic orienteering problem with queueing and time windows, DOPQTW)
我们将该问题建模为马尔可夫决策过程。为了解决计算困难,我们设计了基于rollout算法的近似动态规划方法来确定问题实例的动态解。去往何方或者留在此地的决策根据不同的估计来进行评估。我们称该方法为compound rollout。在compound rollout中,决策由两阶段组成。第一阶段,compound rollour决定是否留在当前地点或是前往下一个地点;如果第一阶段的决策为离开,则第二阶段决定前往何处。
1.2 问题建模
我们将DOPQTW建模为一个马尔可夫决策过程。
我们在一个完全图$G=(V,E)$上定义该问题。$V$中的$n$个节点对应旅行者可能参观的$n$个可能的地点。$E$为连接节点的边的集合。我们假定边$(i,j)$的旅行时间确定,定义为$c_{i,j}$,当$i=j$时$c_{i,j}=0$且满足三角形原则$c_{li}+c_{ij} \leq c_{lj}, \forall i,j,l \in V$。每个节点都带有属性:时间窗$[e_i,l_i]$和奖励$r_i$。
我们假定旅行者出发的足够早,以至于能够在第一个地点的时间窗开始前到达。$M_i$为已知分布的随机变量,表示在地点$i$的服务时间,该分布存在有限上下界$\hat{m}_i$和$\check{m}_i$。$\Psi_i$表示旅行者到达地点$i$的随机变量,$\psi_i$为$\Psi_i$的具体实现。
在每个地点,竞争对手的队列因对手的到达和离开而形成。我们假定此处存在一个最大可能队长$L$。$X_i$为表示对手在地点$i$的到达时间间隔的随机变量,$x_i$为具体实现。$Y_i$为表示对手在地点$i$的服务时间,$y_i$为具体实现。由于旅行者的对手到达和离开不确定,旅行者在队列中的等待时间也为随机。
我们考虑一个离散时间的计划回合$0,1,\cdots,T$,$T=\max_{i\in V}l_i$为决策停止的时间。由于旅行者执行决策的时间点是随机的,因此该动态系统定义了一个半马尔可夫决策过程(semi-Markov decision process)。设$\Xi_k$表示第k个决策的时间点的随机变量,$\xi _k$为具体实现。那么一个决策时间点由下列情况引发:
- 旅行者在前往地点$i$的路上时,下一个决策时间点为当旅行者到达时,$\xi_k = \psi_i$
- 旅行者在地点$i$的队列中等待时,下一个决策时间点发生在下一个队列事件发生时或是一个特定固定时间$\delta$后。$\delta$是旅行者在重新评估去留决策前在队列中将会等待的最长时间。因此,$\xi_k = \xi_{k-1}+ \min {x_i,y_i,\delta}$。
系统状态state为旅行者在当前地点决定去留决策提供了足够信息。状态中包括了旅行者的信息和各个地点的信息:
- 旅行者的信息用三元组$(t,d,q)$表示,$q\in [0,L]$为时刻$t$时旅行者在地点$d\in V$的队长。
- 地点的信息通过将$V$分成三个集合$H,U,W$表示。$H \subset V$表示旅行者已经参观过且收集了奖励的地点;$U \subset V$表示旅行者还未参观的地点;$W \subset V$表示旅行者参观了但还没收集奖励就离开了的地点。对于每个地点$w \in W$,状态包含信息$(\breve{t}_w,\breve{q}_w)$,$\breve{t}_w$表示旅行者离开地点$w$的时间点,$\breve{q}_w$表示离开时的队长。旅行者可以利用这个信息评估是否需要重新参观地点$w \in W$。$(\breve{t},\breve{q})$为总体集合。
因此,我们用$(t,d,q,H,U,W,(\breve{t},\breve{q}))$表示系统的完整状态。状态空间定义在$[0,T]\times V \times [0,L] \times V \times V \times V \times {([0,T],[0,L])}^V$上,初始状态为$s_0=\left ( 0,0,0,\varnothing, V,\varnothing, (\varnothing, \varnothing) \right)$。吸收态(absorbing state)满足以下条件之一:
- 旅行者从所有地点处都收集了奖励
- 旅行者在所有还未收集奖励的地点的时间窗内均无法再到达该地点
因此,吸收态集合定义为$S_K = {(t,d,q,H,U,W,(\breve{t},\breve{q})): H=V \space or \space t + c_{di} \geq l_i, \forall i \in {V \setminus H}}$。
在每个决策时间点,旅行者挑选一个动作决定下一个决策时间点旅行者的位置。在时间$t$地点$d$处,旅行者可以呆在地点$d$或是前往另一个地点$i \in {U \cup W},l_i \geq t+c_{di}$。当$q=0$时旅行者收集到奖励$r_d$。因此,旅行者的动作空间为$A(s)={d} \cup {i \in {U \cup W}: t + c_{di} \leq l_i },if \space q \gt 0$和$A(s)={i \in {U \cup W}: t + c_{di} \leq l_i },if \space q = 0$
1.3 System Dynamics
在选择动作时发生的系统状态变化如图所示。
在决策时间点$k$处,状态为$s_k=(t,d,q,H,U,W,(\breve{t},\breve{q}))$,选中动作$a\in A(s_k)$,状态转变为$s_{k+1}=(t’,d’,q’,H’,U’,W’,(\breve{t}’,\breve{q}’))$。$s_{k+1}$中的$d’=a$就是所选择的动作。令$P(s_{k+1} \mid s_k,a)$为从状态$s_k$选择动作$a$转变为状态$s_{k+1}$的概率。在每个决策时间点,转移概率由两种动作情况定义:
- 旅行者决定离开当前地点,前往另一个地点
- 旅行者决定在当前地点等待,继续排队
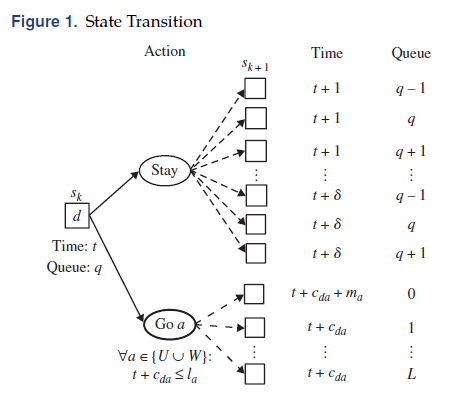
如果选择的动作为前往另一个地点$a$,则$P(s_{k+1} \mid s_k,a)$与到达地点$a$时的时刻$t+c_{da}$时队列长度分布相关。如果队列长度$q’ \gt 0$,则旅行者不能立即收集奖励;否则可以。因此,当选中的动作为前往地点$a$时,$m_a$为服务时间$M_a$的具体实现,我们将当前时间更新为:
\[t' = \left\{\begin{matrix} t+c_{da} & if \space q' \gt 0\\ t+c_{da}+m_a & if \space q'=0 \end{matrix}\right.\]如果选择的动作为留在当前地点$d$,则下一个决策时间点为$t+\min{X_d,Y_d,\delta}$,要么等下一个排队事件发生,要么等一个固定时间$\delta$。排队事件通常为一个新对手的到达,取决于排队规则的设置。在我们的模型中,我们将每个地点的对手的到达间隔时间和服务时间都设置为相同。特别地,旅行者在队列中具有最低优先级,每当一个新的对手到达,它都能排在旅行者前面,旅行者只有等所有对手都服务完后才可以开始服务。
因此,第一个排队事件可能是新对手到达时队伍长度+1,对手离开时队伍长度-1,或者到达和离开同时发生队伍长度不变。如果在$[t,t+\delta]$内无排队事件发生,则队列长度不变。若$t+\min{X_d,Y_d,\delta}$时刻$q’=0$,则旅行者收集奖励$r_d$,然后经历$m_d$服务时间。因此,当选择的动作为待在当前地点时,当前时间更新为
\[t' = \left\{\begin{matrix} t+\min\{X_d,Y_d,\delta\} & if \space q' \gt 0\\ t+\min\{X_d,Y_d,\delta\}+m_d & if \space q'=0 \end{matrix}\right.\]$(t,d,q)$更新完毕,然后开始更新$(H,U,W)$。
\[H' = \left\{\begin{matrix} H & if \space q' \gt 0\\ H \cup \{a\} & if \space q'=0 \end{matrix}\right. \\ U' = \left\{\begin{matrix} U & if \space a=d\\ U \setminus\{a\} & if \space a \neq d \end{matrix}\right. \\ W' = \left\{\begin{matrix} U & if \space a=d\\ U \setminus\{a\} & if \space a \neq d \end{matrix}\right.\]最后我们更新$(\breve{t}’,\breve{q}’)$:如果$q’ \gt 0$,则将$(t’,q’)$加入到$(\breve{t},\breve{q})$中;如果$q’=0$,则从$(\breve{t},\breve{q})$中删去$(t_a,q_a)$
设$\Pi$为该问题所有马尔可夫确定策略的集合。一个策略$\pi \in \Pi$是根据决策规则生成的序列:$\pi = (\rho_0^{\pi}(s_0),\rho_1^{\pi}(s_1),…,\rho_K^{\pi}(s_K))$,$\rho_k^{\pi}(s_k):s_k \to A(s_k)$为从状态映射到动作的函数。我们简称$\rho_k^{\pi}(s_k)$为$\rho_k^{\pi}$。我们需要寻找策略$\pi \in \Pi$最大化总的期望奖励,在初始状态的值为$s_0:E[\sum_{k=1}^KR_k(s_k,\rho^{\pi}(s_k)) \mid s_0]$,$R_k(s_k,a)$为在状态$s_k$时选择动作$a$时收集到的期望奖励。令$V_k(s_k)$表示状态$s_k$的状态价值函数。因此,我们可以在每个决策时间点通过求解$V_k(s_k)=\max_{a\in A(s_k)} { R_k(s_k,a)+E[V_{k+1}(s_{k+1})\mid s_k,a]}$得到最优策略。
1.4 Structural Results
对于许多的不确定环境下的决策问题,存在着最优的控制限制(control limit)或门槛策略(threshold-type policies)。我们在附录中证明了:在特定时间下,假设参观地点的顺序固定时,队伍长度存在着控制限制。也就是说,存在一个门槛队列长度,当观察到该队列长度或更短的长度时待在原地点为最优。虽然我们可以证明这种策略的存在,但在违反固定参观序列假设的动态解决方法中,如何计算阈值或有效地应用这样的阈值并不明显。
在本节剩余部分,我们研究了动作一定为次优的情况。通过删除这种次优的动作,我们能够削减动作空间,改善近似动态规划方法的计算效率。令$o_i(\leq e_i)$表示旅行者的对手在地点$i$处的最早开始排队的时间,我们假定旅行者是了解$o_i$值的。因此,无论排序规则怎样,下列结果均成立:
- 如果旅行者在时刻$t \le o_j - c_{ij}-\hat{m}_i - \delta$处于地点$i$,队列长度为$q \gt 0$,则离开当前地点$i$前往地点$j$的动作应该被删除。(至少可以再等一会,再决定去不去,早去了也只能等)
- 假定队列中的对手不会违约,如果旅行者在时刻$t$且$t + q\hat{m}_i \gt l_i$处于地点$i$,队列长度为$q \gt 0$,则待在原地$i$的动作应该被删除(就算最后等到了也已经过了时间窗)
2.1 Rollout策略
为了找到旅行者的最优策略,我们必须解决每个决策时间点k处状态为$s_k$的最优性方程$V(s_k)=\max_{a \in A(s_k)}{R_k(s_k,a)+E[V(s_{k+1} \mid s_k,a)]}$。由于维度爆炸,准确确定最优策略是不切实际的。因此,我们求助于rollout算法,近似动态规划算法的一种形式。rollout算法通过采用向前的动态规划方法、迭代利用启发式算法策略来估计每个决策时间点的状态价值函数构造rollout策略。
特别地,从第$k$个决策时间点的状态$s_k$开始,rollout算法根据$\hat{V}(s_k)=\max_{a\in A(s_k)}{R_k(s_k,a)+E[\hat{V}(s_{k+1}) \mid s_k,a]}$选择最优动作,此处$\hat{V}(s_{k+1})$由启发式算法进行估计。
A-Priori-Route Policy
为了估计状态价值函数,rollout算法需要一种启发式策略来应用在可能的样本路径上,启发式策略是对于所有未来状态的次优策略。对于DOPQTW而言,我们利用a-priori-route策略来估计状态价值函数。我们选择a-priori-route策略有两个原因:
- a-priori-route策略常常被用于求解动态路由问题中
- a-priori-route策略被证明比其他启发式算法对于应用有随机需求的路由问题的rollout算法更有效
给定状态$s_k$,对应的a-priori-route策略$\pi(v)$的特征为一个priori route $v = (v_1,v_2,\cdots, v_m)$,给定了预制订的旅行者参观$m$个地点的顺序。a priori route在时刻$t$开始于当前地点$d$,状态为$s_k$,跟着$m-1$个地点的序列,地点集合为${{U \cup W} \setminus {d}}$。当前地点$d$的队长信息在状态$s_k$的$q$中。
为了处理在执行priori route中实现的随机信息,我们采用了两种类型的补救动作。第一种补救动作,跳过序列中的下一个地点,灵感源于如果旅行者在一个地点的时间窗内到的比较晚,由于队长他可能不再愿意收集该地点的奖励。第二种补救动作利用了观察到的队长来建立一个静态规则设置旅行者愿意等的最长时间。
我们利用一个变邻域下降从所有与状态$s$相关的路径空间中来搜索一条a priori route。目标是找到一个a priori route $v^{\star}$,代表最优a priori route策略$\pi(v^{\star})$满足$V^{\pi(v^{\star})}(s) \gt V^{\pi(v)}(s)$对于任意的$\pi(v)$。为了减少确切评估$V^{\pi(v^{\star})}(s)$目标值的计算负担,我们利用蒙特卡洛模拟从收集到的临近策略的目标值来估计$V^{\pi(v)}(s)$。
Rollout Algorithm
总而言之,rollout算法通过在每个决策时间点前瞻和利用启发式策略估计价值状态函数来得到rollout策略。取决于rollout步骤中在运用启发式前钱攒的步数,rollout算法也可以分为单步和多步rollout,也有预决策、后决策rollout,可以看作零步和半步前瞻。
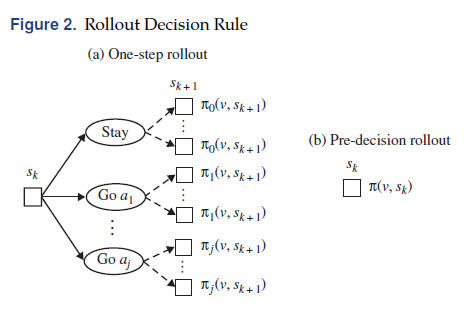
当处于状态$s_k$评估动作$a$时,单步rollout可以转变为在下一个决策时间点所有可能的状态$s_{k+1} \in S(s_k,a)={s_{k+1}:P(s_{k+1} \mid s_k,a) \gt 0}$。对于每一个可能的未来状态$s_{k+1}$,我们通过运行VND算法得到一条a-priori-route策略$\pi(v,s_{k+1})$。在$s_k$处选择动作$a$的状态价值函数估计由a priori route策略在所有可能的状态$s_{t+1}$上的期望值给出。
\[E[V^{\pi(v,s_{k+1})}(s_{k+1}) \mid s_k,a]=\sum_{s_{k+1} \in S(s_k,a)}P(s_{k+1} \mid s_k,a) \times V^{\pi(v,s_{k+1})}(s_{k+1})\]此处$V^{\pi(v,s_{k+1})}(s_{k+1})$为一个a-priori-route策略$\pi(v)$从$s_{k+1}$出发得到的期望值。当进程在第$k$个决策时间点处于状态$s_k$时,它选择动作$a\in A(s_k)$使得$R_k(s_k,a)+E[V^{\pi(v,s_{k+1})}(s_{k+1}) \mid s_k,a]$最大化。对于状态$s_k$和每个可行的动作$a \in A(s_k)$,单步rollout执行启发式搜索$ \mid S(s_k,a) \mid$次。
而pre-decision rollout完全不进行前瞻,而是直接选择在状态$s_k$时的动作。
2.2 Compound Rollout
由于排队过程中的超大状态和动作空间,利用one-step rollout来解决实际大小的算例是十分困难的,甚至将动作的预评估时间限制在一分钟内、加上动作消除规则也不行。
为了说明,考虑$s_k=(t,d,q,H,U,W,(\breve{t},\breve{q}))$和$V(s_k)=\max_{a \in A(s_k)}{R_k(s_k,a) + E[V(s_{k+1}\mid s_k,a)]}=\max{V_{stay}(s_k),V_{go}(s_k)}$,此处$V_{stay}(s_k)=R_k(s_k,d)+E[V(s_{k+1}) \mid s_k,d]$,$V_{go}(s_k)=\max_{a \in {U \cup W \setminus {d}: t+ c_{da} \lt l_a}} E[V(s_{k+1}) \mid s_k,a]$。单步rollout通过前瞻一步执行启发式搜索从$\mid U \cup W \mid \times (L+1)$个可能的状态中寻找$V_{go}(s_j)$的估计值,从$3 \delta$个可能状态中寻找$V_{stay}(s_k)$的估计值。
为了减少单步rollout的计算负担、改善pre-decision rollout的质量,我们提出compound rollout算法。compound rollout通过两阶段过程选择当前时期的动作。在第一阶段,我们比较$\tilde{V}{stay}(s_k)$和$\tilde{V}{go}(s_k)$,两者均为$V_{stay}(s_k)$和$V_{go}(s_k)$的估计值,来决定旅行者是否需要离开。如果$\tilde{V}{stay}(s_k) \lt \tilde{V}{go}(s_k)$,则compoud rollout利用第二阶段来确定下一个参观的地点。否则,旅行者停在当前地点等待直到下一个决策时间点。
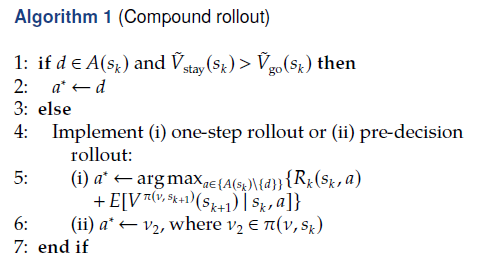
compound rollout的关键在于以一种相对精确但避免过量启发式算法应用的方式来估计$V_{stay}(s_k)$和$V_{go}(s_k)$。在该问题中,我们通过仅仅应用一次启发式算法来计算$\tilde{V}{stay}(s_k)$和$\tilde{V}{go}(s_k)$来实现该目标。
如果待在地点$d$,状态为$s_k$,我们评估期望的状态价值函数为:
\[\tilde{V}_{stay}(s_k) = P(\Omega_{dt} \lt l_d - t \mid q,t) \times r_d + V^{\pi(v,\hat{s}_k)}(\hat{s}_k)\]在该等式中,$\Omega_{dt}$为代表在时间为$t$时在地点$d$队长为$q$的等待时间的随机变量,分布在附录中求到。除此外,在该等式中,$V^{\pi(v,\hat{s}k)}(\hat{s}_k)$是通过a-priori-route策略估计的从状态$\hat{s}_k$出发的期望回报,其中$\hat{s}_k$与$s_k$相同,但$t$被替换为$t+E[\Omega{dt} \mid q,t]$,这是期望的等待时间。
基于等待时间分布和隐式假设(旅行者不会等到时间窗的最后),上述等式可以计算收集到的期望奖励。为了估计在未来收集到的奖励,该等式基于平均等待时间假定了一个分离时间。通过忽视旅行者在时间窗结束前离开的选项,我们承认我们低估了停留动作的状态价值函数。但是后续数值试验中证明了这种影响是有限的。
references
Zhang S, Ohlmann J W, Thomas B W. Dynamic orienteering on a network of queues[J]. Transportation Science, 2018, 52(3): 691-706.
