本文为ADP领域著名研究学者Warren B. Powell在2016年发表于著名期刊 Annals of Operations Research 上。全文介绍了ADP的发展历程、限制与新提出的一系列方法,提出了一个统一的框架。
Abstract
动态规划与不确定性下的时序决策问题相关。尽管它在特定的问题环境下取得了巨大的成功,但我们仍然缺乏具有广泛适用性的通用工具,如线性规划、非线性规划、整数规划等问题中的算法策略。
动态规划的应用已经遍布了各个领域,衍生了不同的名词系统。它们的名字包括马尔可夫决策过程、随机规划、强化学习、Q-learning、随机搜索、模拟优化、启发式动态规划、自适应动态规划、随机控制等等。
根据所考虑的决策变量的类型,我们可以将这部分的研究分为三组:
- Discrete action spaces. 计算机科学与运筹学的部分科研人员集中于解决动作空间较小且离散的情况下的问题,动作空间内通常只有2-100种动作可以选择。这里算法的设计要求枚举所有的动作,但不做连续性或凸性的假设
- Low-dimensional, continuous decisions. 控制工程领域面临着控制设备的问题,其中control的维度数量可能从1到10。但这些问题通常是连续且非凸的
- High-dimensional decisions. 运筹学领域经常处理包含数千到数万个变量的问题。这些问题要么是凸的,要么是利用了诸如整数变量问题的结构,在这些问题中专门设计了算法来搜索高维可行区域
这三类问题都较难求解。可以注意到,随着维度的增加,我们可以利用连续性和凸性这样的性质。因此,只有10个action的问题可能和决策变量有1000个维度但凸性存在的问题难度相同。
这篇文章的目标如下。首先,提供一个从不同领域研究人员视角中ADP的简介。第二,我们详述该领域的发展和不同类问题所提出的挑战。第三,也是最重要的,我们通过鉴定四种基本类型的策略,将大量的算法策略综合起来。最后,我们将介绍基于价值函数近似(value function approximations)的策略,它与术语ADP最广泛地联系在一起。
1 The challenge of dynamic programming
在1957年,Richard Bellman发表了他的开创性著作,提出了解决序列随机优化问题的一个简单而优雅的模型和算法策略。这个问题可以表示如下:寻找一个policy $\pi :\mathcal{S} \rightarrow \mathcal{A}$,将离散状态 $s \in \mathcal{S}$ 映射到一个动作 $a\in \mathcal{A}$,产生贡献 $C(s,a)$。接着,整个系统以概率 $p(s’\mid s,a)$ 转化为新的状态 $s’$ 。如果 $V(s)$ 为状态 $s$ 下的价值,则
\[V(s) = \max_{a\in \mathcal{A}} \left ( C(s,a) + \gamma \sum_{s' \in S}p(s'|s,a)V(s')\right ) \tag{1}\]此处 $\gamma$ 为衰减因子。这就是广为人知的Bellman最优性方程,它表达了Bellman的最优原则,是最优policy的特征。它的出现大大简化了人们对决策树的处理。
决策树的问题在于它们并没有利用多重轨迹可以返回到单一状态的特性。而Bellman的突破正在于可以计算处于某个状态的value,从而将树中表示相同状态的所有节点进行折叠。一旦我们知道了处于某种状态的value,我们只需要通过计算该决策带来的回报加上该决策产生的下一状态的value来评估该决策的价值。对于finite-horizon问题,结果如下
\[V_t(S_t) = \max_{a\in \mathcal{A}} \left ( C(S_t,a) + \gamma \sum_{s' \in S}p(s' \mid S_t,a)V_{t+1}(s')\right ) \tag 2\]等式2往往从某个终端条件例如$V_T(S_T)=0$开始,然后在时间上逐步后退得到所有的动作。
值迭代
对于Infinite-horizon问题,Howard引入了值迭代(value iteration):
\[V^n(s) = \max_{a\in \mathcal{A}} \left ( C(s,a) + \gamma \sum_{s' \in S}p(s'\mid s,a)V^{n-1}(s')\right ) \tag{3}\]该算法能够在具有可证明的界限的极限处收敛,提供了严格的停止规则。等式(1)和(2)都需要至少三重循环:第一重关于状态$S_t$,第二重关于所有动作$a$,第三重关于未来状态$S_{t+1}$。当然,两个算法也需要一步转移概率矩阵$p(s’ \mid s,a)$已知。
对于每一个当前状态$s$,对每个可能的动作$a$都计算一下采取这个动作到达后的下一个状态的期望价值。看看哪个动作可以到达的状态的期望价值函数最大,就将这个最大的期望价值函数作为当前状态的价值函数$V(s)$,循环执行这个步骤,直到价值函数收敛。
策略迭代
值迭代的替代方案是策略迭代。在一个理想世界里,假设我们可以创建一个$S \times S$的矩阵$P^{\pi}$,其元素为$P^{\pi}(s,s’)=p(s’ \mid s,\pi(s))$,此处$a=\pi(s)$由策略$\pi$决定(最好设想为lookup table策略,为每一个状态指定一个离散动作)。令$C^{\pi}$为表示贡献的$S$维向量,每个状态的一个元素为$C(s,\pi(s))$
从一个初始化的策略出发,先进行策略评估,然后改进策略,评估改进的策略,再进一步改进策略,经过不断迭代更新,直达策略收敛,这种算法被称为“策略迭代“。
假设$v^{\pi}$为$S$维向量,其中元素$s$对应从状态$s$开始的steady state value,然后遵循策略$\pi$从现在到无穷大(所有这些理论都假设有一个infinite horizon)。初始时刻的steady state value为:
\[v^{\pi}=(I-\gamma P^\pi)^{-1}c^\pi \tag 4\]而我们经常无法计算这个逆矩阵,因此我们可以换种方式迭代计算:
\[v^m = c^{\pi}+\gamma P^{\pi}v^{m-1} \tag 5\]对于$m=M$的一些情况,我们将会停止,令$v^\pi=v^N$。一旦我们完成了策略价值的评估,我们就可以通过计算每个状态所使用的最优操作来更新策略:
\[a(s)=\arg \max_{a}\left(C(s,a)+\gamma \sum_{s'\in \mathcal{S}}p(s' \mid s,a)v^{\pi}(s')\right) \tag 6\]向量$a(s)$组成了我们通过$\pi$设计的策略。等式(6)也被称为策略迭代
值迭代与策略迭代的区别
值迭代的过程:
- initialization:初始化所有状态的$V(s)$
- find optimal value function:对每一个当前状态$s$,对每个可能的动作$a$,都计算一下采取这个动作后到达的下一个状态的期望价值。看看哪个动作可以到达的状态的期望价值函数最大,就将这个最大的期望价值函数作为当前状态的价值函数$v(s)$循环执行这个步骤,直到价值函数收敛,就可以得到最优optimal的价值函数了
- policy extraction:利用上面步骤得到的optimal价值函数和状态转移概率,就可以计算出每个状态应该采取的optimal动作。
策略迭代的过程:
- initialization:初始化所有状态的$v(s)$以及$\pi(s)$(初始化为随机策略)
- policy evaluation:用当前的$v(s)$对当前策略进行评估,计算每一个状态的$v(s)$,直到$v(s)$收敛,才算训练好了这个状态机制函数$V(s)$
- policy improvement:既然上一步已经得到了当前策略的评估函数V(s),那么就可以利用这个评估函数进行策略改进啦。在每个状态$s$时,对每个可能的动作$a$,都计算一下采取这个动作后到达的下一个状态的期望价值。看看哪个动作可以到达的状态的期望价值函数最大,就选取这个动作。以此更新了$π(s)$,然后再次循环上述2、3步骤,直到$V(s)$与$π(s)$都收敛。
可以发现,策略迭代的第二步policy evaluation与值迭代的第二步find optimal value function十分相似,但后者将最大的期望价值函数(max)保存并迭代更新,前者只更新动作,因此后者可以得到optimal value function,而前者不能得到,但后者收敛速度更快一些。
Curse of dimensionality
维度灾难的问题闻名已久,Bellman本人也在早期动态规划近似的文章中承认了这一点。看上去规模较小的问题,可能拥有着极大的状态空间,这使问题的求解十分困难。但到了今天,Schneider National,美国最大的卡车运输公司之一,旗下拥有着5000多名司机,却通过动态规划成功解决了它的运营问题。每个司机由一个15维的属性向量表示,状态变量有着将近$10^{20}$维。
这是如何发生的呢?我们已经有工具能够解决大规模的动态规划了吗?这个问题不太确切,但我们已经有了一些突破。该领域已经涌现了一些名词,如近似动态规划、强化学习、启发式动态规划等等。与此同时,为特定的问题类设计成功的算法仍然是一种艺术形式。
2 The evolution of dynamic programming
待写。
3 Modeling a dynamic program
我们根据五个核心元素对动态规划进行建模:States, actions, exogenous information, the transition function and the objective function。
我们的优化问题可以写作:
\[\max_{\pi \in \Pi}E^{\pi} \sum_{t=0}^T\gamma ^tC(S_t,A^{\pi}(S_t))\]4 Four classes of policies
在已有的文献中,有四类基本的策略:
- myopic cost function approximations
- lookahead policies
- policy function approximations
- policies based on value function approximations
此外,将两种甚至三种基本策略混合在一起建立一个混合策略也是非常常见的。
4.1 Myopic cost function approximations
Myopic策略最大化一段时期内的贡献,而忽略一个决策对未来的影响。如果我们有一个离散动作$a$,我们可以将该策略写作:
\[A^{\pi}(S_t)=\arg \max_{a\in \mathcal{A}}C(S_t,a)\]Myopic策略可以很好地处理向量值型的决策。通常地,我们也可以将一些可调参数添加到myopic模型中,帮助克服一些更严重的限制。比如,在汽车装卸中,我们可以在贡献中加上加上一个关于延迟时间的惩罚项,来减少汽车的延迟。这也称为“cost function approximation”。
4.2 Lookahead policies
目前也有大部分文献涌现,它们通过在有限的horizon内优化决策来设计策略,以确定现在应该做出的最佳决策。
最常用的Look ahead策略采用了对未来的确定性估计,使它得以处理向量值决策。假设我们在时刻$t$时做出的在$t’$时刻完成的决策为$x_{tt’}$,$c_{t’}$为成本的确定性向量,那么我们需要解决确定的最优化问题:
\[X^{\pi}(S_t|\theta)=\arg \max_t \sum_{t'=t}^{t+T}c_{t'}x_{tt'}\]$\theta$可能表示计划周期$T$。在$S_t$状态的$t$时刻下,我们所采取的最优动作是使得后几个周期内的成本最优的动作。该策略在运筹学研究中称为rolling horizon procedure,在计算机科学中称为receding horizon procedure,在工程控制中称为model predictive control。
然而,这个思想不止于对未来的确定性估计当中。我们也可以在有限的horizon内提出原始的随机优化问题,从而得到:
\[X^{\pi}(S_t|\theta)=\arg \max_{\pi'} E\left ( \sum_{t'=t}^{t+T}C(S_{t'},Y^{\pi}(S_{t'}))\right )\]$Y^{\pi}(S_{t’})$表示我们在决策周期内所使用的决策规则的近似,目的是确定我们需要在$t$时刻完成的决策。正常地来说,我们将T选择得足够小方便解决问题。但因为这样的问题甚至对于T取小值时仍然会爆炸,因此随机规划领域采用了将多周期问题拆分成多个阶段stages的方法,每个阶段stages代表一个获知新信息的时间点。
最常采用的策略是两阶段。第一阶段是”here and now”,此时所有信息都已知;第二阶段可以包含多个时间周期,假定这里存在一个新信息可以开始获知到的单点。令$t=0$表示第一阶段,$t=1,2,…,T$表示第二阶段,这意味着时间 $t=1$ 时的决策可以“看到”未来,但我们只对现在要执行的决策感兴趣。令$\omega$表示可能在第二阶段获知的样本实现,$\Omega$为一个样本。我们的随机规划策略可以写作:
\[X^{\pi}(S_0|\theta)=\arg \max_{x_0,(x_1(\omega),...x_T(\omega))} \left ( c_0x_0 + \sum_{\omega \in \Omega}p(\omega)\sum_{t=1}^Tc_t(\omega)x_t(\omega) \right)\]4.3 Policy function approximations
在很多应用中,策略的结构是十分明显的。比如在股票市场中,当价格高于一定的界限后进行抛售;当库存低于某个点$q$时,补货到固定库存量$Q$。我们可以将我们的库存策略写作:
\[A^{\pi}(S_t \mid \theta)=\left\{\begin{matrix} 0 & if \space S_t \geq q \\ Q-S_t & if \space S_t \lt q \end{matrix}\right.\]找到最优策略也就意味着找到$\theta=(q,Q)$的最优值
在一些其它情况下,我们可能会感觉到state与action之间存在着比较容易定义的关系。例如,游泳池中的出水速度和游泳池的状态水的深度相关,可以用公式表示:
\[A^{\pi}(S_t|\theta)=\theta_0+\theta_1S_t+\theta_2(S_t)^2\]这里,$\pi$就意味着策略函数是一个二次函数。寻找最优策略的过程意味着寻找最优向量$(\theta_0,\theta_1,\theta_2)$。
一个在工程当中非常流行的方法是将策略表示为一个神经网络,如下图所示。神经网络将状态变量的每一维作为输入。而这种方法需要我们对策略进行一定的训练,通常称为”actor-critic”方法。
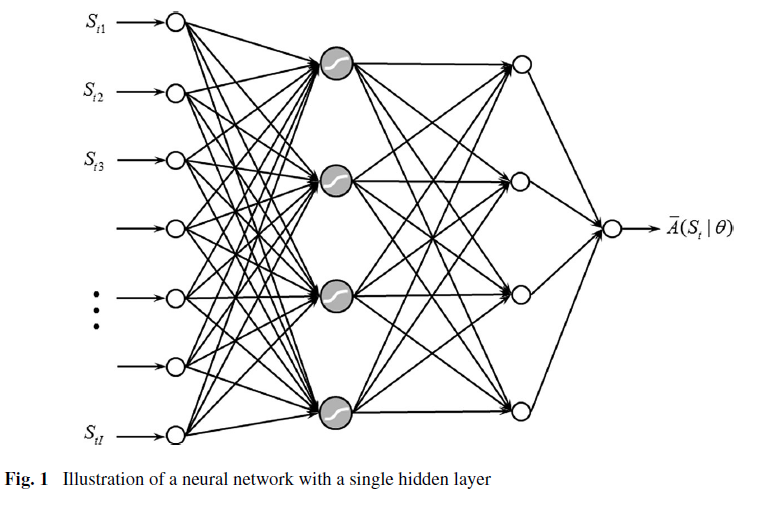
4.4 Policies based on value function approximations
这种方案起源于Bellman等式的期望形式:
\[V(S_t) = \max_{a\in \mathcal{A}}\left ( C(S_t,a) + \gamma E \{ V(S_{t+1}) \mid S_t \} \right )\]此处$S_{t+1} = S^M(S_t,a,W_{t+1})$,$W_{t+1}$为随机变量,可能与$S_t, a$相关。
该等式假定了在给定$V_{t+1}(s)$后,我们可以计算得到每个state $s$ 的$V_t(s)$,且起始点 $s$ 是离散的。如果 $s$ 是一个系数,那么遍历所有的state并不算太难。但当 $s$ 为向量时,潜在的state数量将会随着维数的增加而爆炸。最初的研究(由Bellman和Dreyfus在1959年首次验证)就是用统计近似来代替价值函数,而后直到1970年,控制工程领域的科学家们开始使用神经网络拟合价值函数的近似。
当用线性统计模型来代替价值函数时,这个想法获得了极大的支持。在ADP的语言中,令$\phi_f(S_t)$为基函数,$(\phi_f(S_t)),f\in \mathcal{F}$为features的集合。我们可以将我们的价值函数近似写作:
\[\bar{V}(S_t \mid \theta)=\sum_{f\in \mathcal{F}}\theta_f\phi_f(S_t)\]我们现在将估计每个状态 $S_t$ 的价值 $V(S_t)$ 的问题简化为了估计向量 $(\theta_f)_{f\in \mathcal{F}}$ 的问题
接下来,我们将设计一种方法来估计这个近似值。最初的想法是,我们可以用避免遍历所有状态的方程来替换向后的动态规划方程如(2)和(3)。而这个想法并不是在时间上向后走,而是向前走,利用价值函数的近似来指导决策。
假定我们正在解决一个finite horizon的问题,使时间索引显式:
\[\bar{V}_t^{n-1}(S_t)=\sum_{f\in \mathcal{F}}\theta_{tf}^{n-1}\phi_{tf}(S_t) \tag{16}\]是 $t$ 时刻在 $n-1$ 次观测后的价值函数近似。现在假设我们处于单一状态 $S_t^n$,我们可以计算处于该状态下的价值的估计:
\[\hat{v}_t^n=\max_a \left( C(S_t^n,a) + \gamma\sum_{s'}p(s' \mid S^n,a)\bar{V}_{t+1}^{n-1}(S_{t+1}) \right )\]设 $a_t^n$ 为上述问题的解。我们利用这个等式的右边项来更新我们对该状态的价值的估计。现在,我们建议使用 $\hat{v}_t^n$ 作为样本观测值来更新我们对值函数的近似。如果我们使用离散的查找表表示,可以使用状态 $S_t^n$ 的价值估计 $\bar{V}_t^{n_1}(S_t^n)$:
\[\bar{V}_t^n(S_t^n) = (1-\alpha_{n-1})\bar{V}_t^{n-1}(S_t^n)+\alpha_{n-1}\hat{v}_t^n\]$\alpha_{n-1}$为步长(也称为平滑因子或学习速率,小于等于1)。如果我们使用像式(16)一样的线性回归模型,我们可以利用递归最小二乘法来更新$\theta_t^{n-1}$。线性回归的优势在于我们并不需要检查每一个state,因为我们所要做的是估计回归因子 $\theta_t$。这个算法策略与值迭代非常近似,所以也称作 approximate value iteration
