该节内容摘自于《动手学强化学习》第5章 时序差分算法。
算法简介
前面介绍的动态规划算法要求马尔可夫决策过程是已知的,即要求与智能体交互的环境是完全已知的(例如迷宫或者给定规则的网格世界)。在此条件下,智能体其实并不需要和环境真正交互来采样数据,直接用动态规划算法就可以解出最优价值或策略。这就好比有监督学习任务,如果直接显式地给出了数据的分布公式,那么也可以通过在期望层面上直接最小化模型的泛化误差来更新模型参数,并不需要采样任何数据点。
但这在大部分场景下并不现实,机器学习的主要方法都是在数据分布未知的情况下针对具体的数据点来对模型做出更新的。对于大部分强化学习现实场景(例如电子游戏或者一些复杂物理环境),其马尔可夫决策过程的状态转移概率是无法写出来的,也就无法直接进行动态规划。在这种情况下,智能体只能和环境交互,通过采样到的数据来学习,这类学习方法统称为无模型的强化学习。
不同于动态规划算法,无模型的强化学习算法不需要事先知道环境的奖励函数和状态转移函数,而是直接使用和环境交互的过程中采样的数据来学习,这使得它可以被应用到一些简单的实际场景中。本章将要讲解无模型的强化学习中的两大经典算法:Sarsa和Q-learning,它们都是基于时序差分(temporal difference, TD)的强化学习算法。
同时,本章还会引入一组概念:在线策略学习和离线策略学习。通常来说,在线策略学习要求使用在当前策略下采样得到的样本进行学习,一旦策略被更新,当前的样本就被放弃了,就好像在水龙头下用自来水洗手;而离线策略学习使用经验回放池将之前采样得到的样本收集起来再次利用,就好像使用脸盆接水后洗手。因此,离线策略学习往往能够更好地利用历史数据,并具有更小的样本复杂度(算法达到收敛结果需要在环境中采样的样本数量),这使其被更广泛地应用。
时序差分方法
时序差分是一种用来估计一个策略的价值函数的方法,它结合了蒙特卡洛和动态规划算法的思想。时序差分方法和蒙特卡洛的相似之处在于可以从样本数据中学习,不需要事先知道环境;和动态规划的相似之处在于根据贝尔曼方程的思想,利用后续状态的价值估计来更新当前状态的价值估计。
回顾一下蒙特卡洛方法对价值函数的增量更新方式:
\[V(s_t)\leftarrow V(s_t)+\alpha[G_t-V(s_t)]\]这里我们将$\frac{1}{N(s)}$替换成了$\alpha$,表示对价值估计更新的步长。可以将$\alpha$取为一个常数,此时更新方式不再像蒙特卡洛方法那样严格地取期望。蒙特卡洛方法必须等整个序列结束之后才能计算得到这一次的回报$G_t$,而时序差分方法只需要当前步结束即可进行计算。具体来说,时序差分算法用当前获得的奖励加上下一个状态的价值估计来作为在当前状态会获得的回报,即:
\[V(s_t)\leftarrow V(s_t)+\alpha[r_t+\gamma V(s_{t+1}) - V(s_t)]\]其中,$R_t+\gamma V(s_{t+1}) - V(s_t)$通常被称为时序差分(temporal difference, TD)误差。可以用$r_t+\gamma V(s_{t+1})$来代替$G_t$的原因是:
\[\begin{align*} V_{\pi}(s) &= E_{\pi}[G_t \vert S_t=s] \\ &= E_{\pi}[\sum_{k=0}^{\infty}\gamma^k R_{t+k} \vert S_t=s] \\ &= E_{\pi}[R_t+\gamma \sum_{k=0} \gamma^k R_{t+k+1} \vert S_t=s] \\ &= E_{\pi}[R_t+\gamma V_{\pi}(S_{t+1}) \vert S_t=s] \end{align*}\]因此,蒙特卡洛方法将上式第一行作为更新的目标,而时序差分算法将上式最后一行作为更新的目标。于是,在用策略和环境交互时,每采样一步,我们就可以使用时序差分算法来更新状态价值估计。时序差分算法用到了$V(s_{t+1})$的估计值,可以证明它最终收敛到策略$\pi$的价值函数,我们在此不对此进行展开说明。
Sarsa算法
既然我们可以用时序差分方法来估计价值函数,那一个很自然的问题是,我们能够用类似策略迭代的方法来进行强化学习。策略评估已经可以通过时序差分算法实现,那么在不知道奖励函数和状态转移函数的情况下该如何进行策略提升?答案是可以直接用时序差分算法来估计动作价值函数$Q$:
\[Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha[r_t+\gamma Q(s_{t+1}, a_{t+1})-Q(s_t, a_t)]\]然后我们用贪婪算法来选取在某个状态下动作价值最大的那个动作,即$\argmax_a Q(s,a)$。这样似乎已经形成了一个完整的强化学习算法:用贪婪算法根据动作价值选取动作来和环境交互,再根据得到的数据用时序差分算法更新动作价值估计。
然而,这个简单的算法存在两个需要进一步考虑的问题。第一,如果要用时序差分算法来准确地估计策略的状态价值函数,我们需要用极大量的样本来进行更新。但实际上我们可以忽略这一点,直接用一些成本来评估策略,然后就可以更新策略了。第二,如果在策略提升中一直根据贪婪算法得到一个确定性的策略,可能会导致某些状态动作对$(s, a)$永远没有在序列中出现,以至于无法对其动作价值进行估计,进而无法保证策略提升后的策略比之前的好。我们在第2章中对此有详细讨论。简单常用的解决方案是不再一味使用贪婪算法,而是采用一个$\epsilon$-贪婪策略;
现在我们就可以得到一个实际的基于时序差分方法的强化学习算法。这个算法被称之为Sarsa,因为它的动作价值更新用到了当前状态s,当前动作a,获得的奖励r,下一个状态s和下一个动作a

多步Sarsa算法
蒙特卡洛方法利用当前状态之后每一步的奖励而不使用任何价值估计,时序差分算法指利用一步奖励和下一个状态的价值估计。那它们之间的区别是什么呢?总的来说,蒙特卡洛方法是无偏(unbiased)的,但是具有比较大的方差,因为每一步的状态转移都具有不确定性,而每一步状态采取的动作所得到的不一样的奖励最终都会加起来,这会极大影响最终的价值估计;时序差分算法具有非常小的方差,因为只关注了一步状态转移,用到了一步的奖励,但是它是有偏的,因为用到了下一个状态的价值估计而不是真实的价值。那有没有什么方法可以结合二者的优势呢?答案是多步时序差分!多步时序差分的意思是使用$n$步的奖励,然后使用之后的状态的价值估计,即:
\[G_t = r_t+\gamma r_{r+1} + \cdots + \gamma ^n Q(s_{t+n}, a_{t+n})\]因此,多步Sarsa算法中的动作价值函数更新公式为:
\[Q(s_t, a_t) \leftarrow Q(s_t,a_t) + \alpha[r_t+\gamma r_{t+1} + \cdots + \gamma^n Q(s_{t+n}, a_{t+n}) - Q(s_t, a_t)]\]Q-learning算法
除了Sarsa,还有一种非常著名的基于时序差分算法的强化学习算法——Q-learning。Q-learning和Sarsa的区别在于Q-learning的时序差分更新方式为:
\[Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha [R_t + \gamma \max_a Q(s_{t+1}, a) - Q(s_t, a_t)]\]Q-learning算法的具体流程如下:

在线策略算法与离线策略算法
我们称采样数据的策略为行为策略(behavior policy),称用这些数据来更新的策略为目标策略(target policy)。在线策略(on-policy)算法表示行为策略和目标策略是同一个策略;而离线策略(off-policy)算法表示行为策略和目标策略不是同一个策略。Sarsa是典型的在线策略算法,而Q-learning是典型的离线策略算法。判断二者类别的一个重要手段是看计算时序差分的价值目标的数据是否来自当前的策略:
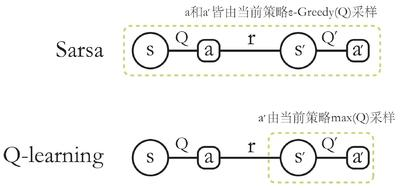
- 对于Sarsa,它的更新公式必须来自当前策略采样得到的五元组(s0,a0,r,s1,a1),因此它是在线策略学习方法
- 对于Q-learning,它的更新公式使用的是四元组(s0, a0, r, s1),该四元组并不需要是当前策略采样得到的数据,也可以来自行为策略,因此它是离线策略算法
