1. 文章背景
本文主要对Mt/M/ct的排队系统进行建模。其中,顾客到达时间符合参数为$\lambda_t$的泊松分布,服务时间符合参数为$\mu$的负指数分布。本文对时变需求的处理方法是:将一天划分为多个时段,不同时段间到达率不同,同一时段内到达率恒定。
2. 均匀化建模
均匀化的方法由Winfried Grassmann于1977年提出,用于将有限状态的连续时间马尔可夫链(CTMC, continuous-time Markov chain)转化为离散时间马尔可夫链(DTMC, discrete-time Markov chain)。考虑一个CTMC,其所有状态的转出速率均相同为$\beta$,我们用$P_{ij}(t)$来表示在0时刻处于状态$i$的条件下,$t$时刻处于状态$j$的概率,即
\[P_{ij}(t) = P\{X(t) = j \vert X(0) = i\} \tag{1}\]根据全概率公式,我们可以将公式(1)转化为如下形式,假设$N(t)$为从0到t的状态转移次数
\[P_{ij}(t) = \sum_{n = 0}^{\infty} \left[ P\{X(t) = j \vert X(0) = i, N(t) = n\} \times P\{N(t) = n \vert X(0) = i\}\right] \tag{2}\]根据泊松过程的性质,我们可以得到
\[P_{ij}(t) = \sum_{n = 0}^{\infty} \left[ P\{X(t) = j \vert X(0) = i, N(t) = n\} \times \frac{(\beta t)^n}{n!} e^{-\beta t} \right] \tag{3}\]由于每一种状态的转出速率均相同,而$N(t) = n$并没有给我们额外的关于在$t$时间内哪些状态被访问的信息,因此有
\[P_{ij}(t) = \sum_{n=0}^{\infty} \left[ P_{ij}(n) \times \frac{(\beta t)^n}{n!} e^{-\beta t}\right] \tag{4}\]其中,$P_{ij}(n)$为一个等价的DTMC从状态$i$到状态$j$的$n$步转移概率。根据公式(4),我们可以通过0时刻的系统状态计算出在$t$时刻每一种状态出现的概率。不过需要注意到,公式(4)的使用条件包括所有状态的转出速率相同,因此对于转出速率不同的马尔可夫链,往往需要添加一种虚拟的状态转移–将某种状态转移到这种状态本身,并设置这种自转移的概率使所有状态的转出速率都与原马尔可夫链的最大转出速率相等。
而利用这种方法,我们可以在已知时段开始时系统所处的状态和时段的长度已知的情况下,利用该公式直接得到时段结束时系统的状态(此处状态是指处于每种状态的概率)。我们将系统人数$q$作为系统状态的表现指标,则可以将M/M/c的排队系统转化为以下马尔可夫链:
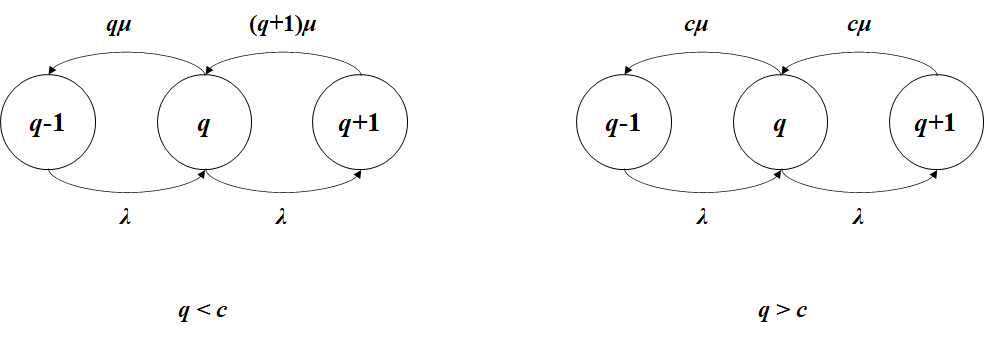
该马尔可夫链可以分为两种情况进行考虑:当系统中的人数$q$小于服务台数目$c$小时,顾客离开的速率(即生灭过程中“灭”的速率)与状态参数的大小相关。而当系统人数$q$比服务窗数目$c$大时,顾客离开的速率为定值。
注意到,每种状态的转出概率不同,最大为$\lambda + c\mu$,因此需要为转出速率较小的状态($q < c$)添加虚拟的状态转移
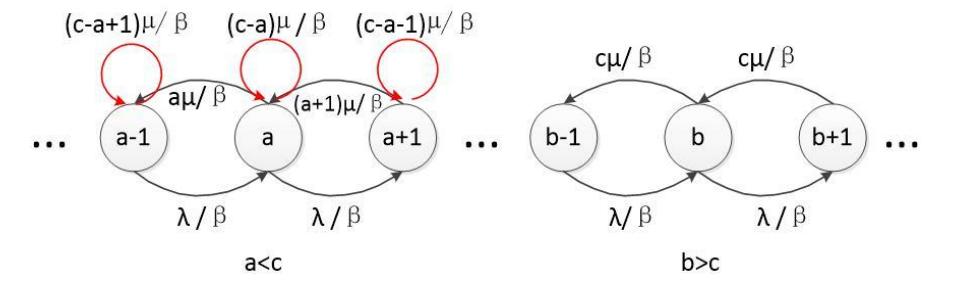
添加虚拟转移后,所有状态的转出速率均为$\lambda + c\mu$,满足公式(4)的使用条件,此时$\beta = \lambda + c\mu$,因此有
为了计算方便,对其进行一些近似处理:
\[P_{ij}(t) = \sum_{n = 0}^N \left[ P_{ij}(n) \times \frac{(\beta t)^n}{n!} e^{-\beta t} \right], i \& j < qm \tag{5}\]此处对公式(4)做了两处近似处理:一是将可能的最大状态转移步数将无穷变成$N$($N$的大小取决于具体情况),由于转出速率$\beta$的限制,因此在给定时间$t$内系统发生的状态转移(包括虚拟的自转移)总是有限的,因此该处近似处理影响不大;二是将可能的系统状态数目从无穷变为了$qm$,因为顾客到达率$\lambda$的影响,在给定时间$t$内系统中的顾客数目同样不会是无穷多的,因此这种近似不会对结果带来太大的影响。
在公式(5)中,目前只有$P_{ij}(n)$是未知的,我们下面探讨如何求解$P_{ij}(n)$。显然,$n$步转移概率可以通过$n-1$步转移概率可能的情况进行递推。而对于第$n$步转移到状态$j$,只可能有以下三种情况:
-
系统的状态参数增加
对应一个新的顾客进入系统,系统参数$q$从$j-1$增加到$j$。当$j-1$小于$qm$时,系统处于任何状态时一次状态转移为状态参数增加的概率为$\lambda / \beta$。因此 \(P_{ij}^{(1)}(n)=P_{i,j-1}(n-1) \times \frac{\lambda}{\beta} \tag{6}\)
-
系统的状态参数减少
对应一个系统中的顾客离开系统,系统参数$q$从$j+1$减少到$j$。因此 \(P_{ij}^{(2)}(n)=P_{i,j+1}(n-1) \times \frac{\min\{c,j+1\} \mu }{\beta} \tag{7}\)
-
系统的状态参数不变 对应系统发生了一次虚拟的自转移,系统参数$q$从$j$变到$j$。 \(P_{ij}^{(3)}(n)=P_{ij}(n-1)\times \frac{c\mu - \min\{c,j\}\mu}{\beta} \tag{8}\)
综上,第$n$步转移到状态$j$的概率为
\[\begin{align*} P_{ij}(n) &= P_{ij}^{(1)}(n)+P_{ij}^{(2)}(n)+P_{ij}^{(3)}(n) \\ & = P_{i,j-1}(n-1) \times \frac{\lambda}{\beta} + P_{i,j+1}(n-1) \times \frac{\min\{c,j+1\} \mu }{\beta} + P_{ij}(n-1)\times \frac{c\mu - \min\{c,j\}\mu}{\beta} \end{align*} \tag{9}\]在公式(9)中,我们忽略了第$n-1$步处于0和$qm$的特殊情况。如果系统在$n$次状态转移后处于状态0,则第$n-1$次状态转移只可能是自转移或者状态参数减少;如果系统在$n$次状态转移后处于状态$qm$,则第$n-1$次状态转移只可能是自转移或者状态参数增加(假定$qm > c$)
\[P_{i0}(n) = P_{i1}(n-1) \times \frac{\mu}{\beta} + P_{i0}(n-1) \times \frac{c\mu}{\beta} \tag{10}\] \[P_{i,qm}(n) = P_{i,qm-1}(n-1) \times \frac{\lambda}{\beta}+ P_{i,qm}(n-1) \times \frac{\lambda}{\beta} \tag{11}\]结合(9)、(10)、(11),我们可以得到该系统的状态转移矩阵:
\[P_{(qm+1)(qm+1)}= \begin{bmatrix} \frac{c\mu}{\beta} & \frac{\lambda}{\beta} & 0 & \cdots & 0 & 0 & 0 \\ \frac{\mu}{\beta} & \frac{(c-1)\mu}{\beta} & \frac{\lambda}{\beta} & \cdots & 0 & 0 & 0 \\ 0 & \frac{\min(c,2)\mu}{\beta} & \frac{c\mu - \min(c,2)\mu}{\beta} & \cdots & 0 & 0 & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & 0 & \cdots & \frac{c\mu - \min(c,qm-2)\mu}{\beta} & \frac{\lambda}{\beta} & 0 \\ 0 & 0 & 0 & \cdots & \frac{\min(c,qm-1)\mu}{\beta} & \frac{c\mu- \min(c,qm-1)\mu}{\beta} & \frac{\lambda}{\beta} \\ 0 & 0 & 0 & \cdots & 0 & \frac{\min(c,qm)\mu}{\beta} & \frac{\lambda + (c - \min(c,qm))\mu}{\beta} \end{bmatrix} \tag{12}\]此时,我们只需要将时段开始时系统所处的状态用$1 \times (qm + 1)$的矩阵$A_t$表达出来($A_t$的每一个元素代表系统初始处于对应状态的概率),就可以得到在该时段结束时系统所处的状态(同时也是下个时段开始时系统所处的状态)$A_{t+1}$
\[A_{t+1} = A_t \times \sum_{n=0}^N \left( P^n \times \frac{(\beta t)^n}{n!} e^{-\beta t}\right) \tag{13}\]由于我们选择采用系统中的人数$q$表示系统参数,$A_{t+1}$表示了一个时段结束时系统中人数的概率分布,因此我们可以得到系统人数的期望
\[E_t(q) = \sum_{i=0}^{qm} i \times A_{t+1}(i) \tag{14}\]3. 对总等待时间的近似
在上一节中,我们在介绍均匀化公式时引入了状态转移次数$N(t)$的概念,并出于简化计算的需要给$N(t)$设定了一个最大值$N$。但需要强调的是,均匀化方法中在一个时段$t$内的系统并非经历了$N$次系统转移,而是经历了不多于$N$次的状态转移,具体的状态转移次数是未知的,只能通过泊松分布的性质求出每种情况出现的概率。
因此,在求解系统在一个时段内所有顾客的总等待时间时,我们可以根据状态转移次数的情况进行分类:
\[wt = \sum_{k=0}^N \left\{ P(N(t) = k \vert X(0) = ini) \times E(wt \vert N(t) = k, X(0) = ini) \right\} \tag{15}\]公式(15)中的wt表示总等待时间,ini表示在时段开始时系统所处的初始状态。由上一节可知,这种状态并不是确定的,而是由系统处于各状态的概率组成的矩阵,因此在以下推导中我们不会对这部分加以强调。
公式(15)中的前半部分可以根据泊松过程的性质求得:
\[P(N(t) = k \vert X(0) = ini) = \frac{\beta^k}{k!} e^{-\beta} \tag{16}\]因此,我们将重心放在公式(15)的后半部分。现在假定一个排队系统,在一个长度为$T$的时段内固定发生了$k$次转移,由于均匀化添加了虚拟的自转移来保证每个状态的转出速率都相同,因此每次转移所消耗的时间是相等的:
\[t_{transition} = \frac{T}{k+1} \tag{17}\]注意到,分母是$k+1$而不是$k$,这是由于每次转移所消耗的时间实际上是指在每一个状态停留的时间。考虑$k = 0$的情况,系统在初始状态停留的时间为整个时段的长度$T$。总的等待时间必定与等待的人数相关。现在我们假定:在系统停留在某一状态时系统中的人数为$i$,则需要等待的顾客的数目为$\max{i - c, 0}$。
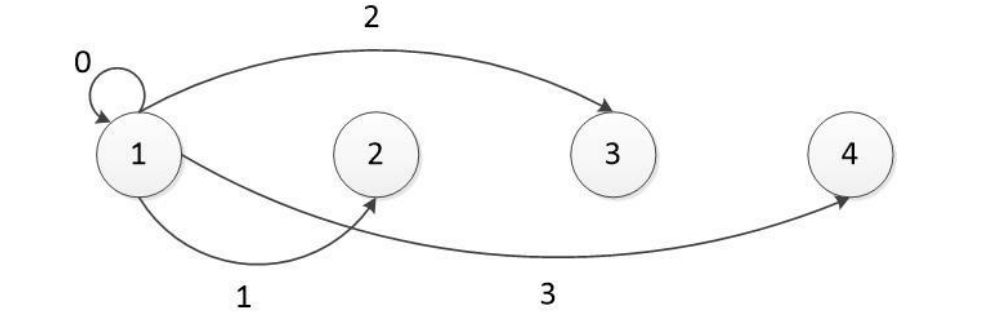
为了方便说明,在此给出一个$k = 3$的例子。每个状态持续的时间为$T/4$。状态1是已知的初始状态ini,箭头0表示了i个顾客出现在第一个状态的概率,也就是发生了0次状态转移后系统状态由ini变为i的概率,也就是上一节中的$P_{ini,i}(0)$;箭头1表示了i个顾客出现在第二个状态的概率,也就是发生了1次状态转移后系统状态由ini变成i的概率$P_{ini, i}(1)$;同理,箭头2和3分别代表了$P_{ini,i}(2)$和$P_{ini, i}(3)$。i个顾客出现在该时段的每个状态的概率为上述几个概率的和。
同理,我们可以得到在已知系统发生了$k$次状态转移时,其总等待时间的期望为
\[E(wt \vert N(t) = k, X(0) = ini) = \sum_{i = 0}^{qm} \left[ \max\{i - c, 0\} \times\frac{T}{k+1} \times \sum_{m = 0}^k P_{ini,i}(m) \right] \tag{18}\]因此,根据公式(15)、(16)、(18),我们可以推出均匀化方法对时段内总等待时间的近似为
\[wt = \sum_{k = 0}^N \left\{ \frac{\beta^k}{k!}e^{-\beta} \times \sum_{i = 0}^{qm} \left[ \max\{i - c, 0\} \times \frac{T}{k+1} \times \sum_{m=0}^k P_{ini,i}(m) \right] \right\} \tag{19}\]