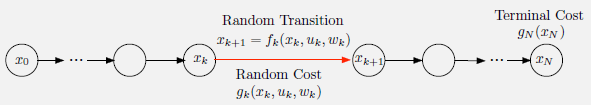该节内容摘自于《Reinforcement Learning and Optimal Control》Chapter 1 Exact Dynamic Programming。
1.1 确定动态规划
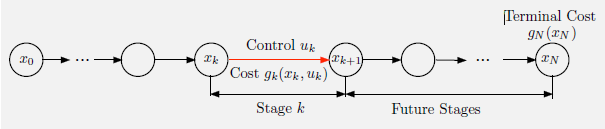
所有的动态规划问题中都存在一个离散时间的动态系统,在控制的影响下产生了一个状态序列。在有限阶段问题中,系统在有限的步数$N$(也称为阶段)下逐步演化。在时刻$k$的状态与控制分别表示为$x_k$和$u_k$。确定性系统的一个特点在于:$x_{k+1}$并非随机产生的,它取决于$x_k$和$u_k$的值。
确定系统往往表示为:
\[x_{k+1} = f_k(x_k, u_k), \quad k=0,1,...,N-1 \tag{1.1}\]$k$是时间索引,$x_k$是系统的状态,$u_k$是控制或决策变量,是在时刻$k$需要从集合$U_k(x_k)$中选取的动作,而$f_k$是将$(x_k,u_k)$映射到$x_{k+1}$的函数。
在时刻$k$所有可能的状态$x_k$称为状态空间(state space),而所有可能的控制$u_k$称为控制空间(control space)。除此外,该问题还包含一个成本函数用来表示在时刻$k$即时产生的成本,记为$g_k(x_k,u_k)$,随着时间累积。对于给定的初始状态$x_0$,控制序列${u_0,…,u_{N-1}}$的总成本为
\[J(x_0;u_0,...,u_{N-1})=g_N(x_N)+\sum_{k=0}^{N-1}g_k(x_k,u_k) \tag{1.2}\]$g_N(x_N)$是在过程结束时刻产生的成本。我们想要在满足控制约束的同时最小化(1.2)中的总成本,从而获得最优值。
\[J^\star(x_0)= \min_{u_k \in U_k(x_k)}J(x_0;u_0,...,u_{N-1})\]离散最优控制问题
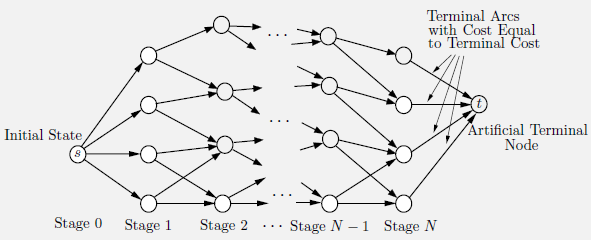
在很多情况中,状态state与控制control都是自然离散的,在有限范围内取值,往往可以便利地表示为一个无环图。图的节点对应了状态$x_k$,而边则对应了$(x_k,u_k)$。所有的控制序列都从$s$出发,在经过$N$步后最终到达$t$。如果我们将一条边的成本看作是它的长度,那么我们就会发现:确定性有限状态有限阶段问题是等价于在起始节点和终止节点间找一条最短路的。我们定义一条路径为由边组成、每两条边首尾相连的集合,一条路径的长度也就是它的所有边的长度总和。通常来说,组合优化问题都可以被转化为一个确定性有限状态有限阶段的最优控制问题。
连续空间最优控制问题
控制理论中的许多经典问题中状态都属于Euclidean space,即$n$维实数变量的向量空间。
动态规划算法
DP算法的核心在于最优性原则:
令${u_0^\star,…,u_{N-1}^*}$表示最优的控制序列,和$x_0$一起决定了相应的状态序列${x_1^\star,…,x_N^\star}$。考虑如下的子问题:我们起始于时刻$k$时的状态$x_k^\star$,希望最小化从时刻$k$到时刻$N$的“cost to go”: \(g_k(x_k^\star,u_k)+\sum_{m=k+1}^{N-1}g_m(x_m,u_m)+g_N(x_N)\) 那么截断后的最优控制序列${u_k^\star,…,u_{N-1}^\star}$对于子问题仍是最优的。
最优性原则表明了:一个最优序列的局部序列对于子问题而言仍是最优的。最优成本函数可以按照逐点向后的方式来进行构造:首先计算涉及最后一阶段的子问题,然后求解涉及最后两阶段的子问题,以此类推,知道构造出整个问题的最优成本函数。
在DP算法中,构造函数$J_N^\star(x_N),J^\star_{N-1}(x_{N-1}),…,J_0^\star(x_0)$。$J_k^\star(x_k)$是对于一个开始于时刻$k$的状态$x_k$、终止于时刻$N$的$(N-K)$阶段子问题的最优成本。对于任意的$x_N$,
\[J_N^\star(x_N)=g_N(x_N) \tag{1.3}\]对于$k=0,…,N-1$
\[J_k^\star(x_k)=\min_{u_k \in U_k(x_k)} \left [ g_k(x_k,u_k) + J_{k+1}^\star(f_k(x_k,u_k))\right ], \forall x_k \tag{1.4}\]我们从$J_{N}^\star$开始计算,一步步推回到$J_0^\star(x_0)$。对于每一个初始状态$x_0$,在最后一步得到的$J_0^\star(x_0)$都等于最优成本$J^\star(x_0)$。实际上,更普遍地,对于任意的$k=0,1,…,N-1$和时刻$k$时的状态$x_k$,我们有
\[\begin{align} J_k^\star(x_k) &= \min_{u_k \in U_k(x_k)}\left [ g_k(x_k,u_k) + J_{k+1}^\star (f_k(x_k,u_k)) \right ] \\ &= \min_{u_k \in U_k(x_k)}\left [ g_k(x_k,u_k) + \min_{u_m \in U_m(x_m),m=k+1,...,N-1}\left [ g_N(x_N) + \sum_{m = k + 1}^{N-1} g_m(x_m,u_m)\right ] \right ] \\ &= \min_{u_m \in U_m(x_m),m=k,...,N-1}g_N(x_N)+\sum_{m=k}^{N-1}g_m(x_m,u_m) \\ &=\min_{u_m \in U_m(x_m),m=k,...,N-1}J(x_k;u_k,...,u_{N-1}) \tag{1.5} \\ \end{align}\]注意到在该算法中每一个子问题都得到了解决。一旦函数$J_0^\star,…,J_N^\star$得到,我们就可以利用如下算法来对给定的初始状态$x_0$构造最优的控制序列${u_0^\star,…,u_{N-1}^\star}$和相应的状态路径${x_1^\star,…,x_N^\star }$。
Construction of Optimal Control Sequence ${u_0^\star,…,u_{N-1}^\star}$
Set \(u_0^\star \in \arg \min_{u_0\in U_0(x_0)} \left [ g_0(x_0,u_0) + J_1^\star (f_0(x_0,u_0))\right ]\) and \(x_1^\star =f_0(x_0,u_0^\star)\) Sequentially, going forward, for $k=1,2,…,N-1$, set \(u_k^\star \in \arg \min_{u_k\in U_k(x_k^\star)} \left [ g_k(x_k^\star,u_k) + J_{k+1}^\star (f_k(x_k^\star,u_k))\right ]\) and \(x_{k+1}^\star =f_k(x_k^\star,u_k^\star)\)
值空间近似
上面所提到的正向的最优控制序列构造需要在通过DP计算所有的$x_k$和$k$的$J^\star_k(x_k)$之后才能完成。而这需要耗费大量的时间,因为$x_k$和$k$的可能取值或许非常之多。而一个类似的向前计算过程可以利用对最优cost-to-go函数$J_k^\star$进行近似$\tilde{J}_k$来得到。这就是值空间近似的基本思想。
在值空间近似中,我们可以构造一个次优解${\tilde{u}0,…,\tilde{u}{N-1}}$来替代最优解${u_0^\star,…,u_{N-1}^\star }$。
Approximation in Value Space - Use of $\tilde{J}_k$ in Place of $J_k^{\star}$
Set \(\tilde{u}_0 \in \arg \min_{u_0\in U_0(x_0)} \left [ g_0(x_0,u_0) + \tilde{J}_1 (f_0(x_0,u_0))\right ]\) and \(\tilde{x}_1 =f_0(x_0,\tilde{u}_0)\) Sequentially, going forward, for $k=1,2,…,N-1$, set \(\tilde{u}_k \in \arg \min_{u_k\in U_k(\tilde{x}_k)} \left [ g_k(\tilde{x}_k,u_k) + \tilde{J}_{k+1} (f_k(\tilde{x}_k,u_k))\right ]\) and \(\tilde{x}_{k+1} =f_k(\tilde{x}_k,\tilde{u}_k)\)
Q因子与Q学习
我们通常也定义$\tilde{Q}k(x_k,u_k)=g_k(x_k,u_k) + \tilde{J}{k+1}(f_k(x_k,u_k))$,也被称为$(x_k,u_k)$的(近似)Q因子。近似最优控制可以通过最小化Q因子来实现。
1.2 随机动态规划
随机有限阶段最优控制问题和确定问题主要的不同点在于离散动态系统对$x_k$演化的处理不同。在随机问题中,该系统包含了一个随机的“扰动”$w_k$,概率分布为$P_k(\cdot \vert x_k,u_k)$。系统的形式为:
\[x_{k+1} = f_k (x_k,u_k,w_k), \quad k=0,1,...,N-1\]每个阶段的成本表示为$g_k(x_k,u_k,w_k)$。一个重要的区别在于我们不再在控制序列${u_0,…,u_{N-1}}$上进行优化,而是在策略(policies)上进行优化。策略由一个函数序列组成:
\[\pi = \{\mu_0,...,\mu_{N-1}\}\]$\mu_k$为将状态$x_k$映射到控制$u_k=\mu_k(x_k)$的函数,并满足控制约束,称为可行的策略。
另一个重要的不同点在于:在随机问题中,成本函数的值包含了可能的期望值,这可能需要通过Monte Carlo模拟来实现。给定初始状态$x_0$和一个策略$\pi={\mu_0,…,\mu_{N-1}}$,未来状态$x_k$和扰动$w_k$均为随机变量。因此,对于给定的函数$g_k,k=0,1,…,N$,开始于$x_0$的$\pi$的期望成本为:
\[J_\pi(x_0)= E\left \{ g_N(x_N) + \sum_{k=0}^{N-1}g_k(x_k,\mu_k(x_k), w_k)\right \}\]而一个最优策略$\pi^\star$是最小化该成本的策略,$J_{\pi^\star}(x_0) = \min_{x \in \Pi} J_{\pi}(x_0)$。
有限阶段随机动态规划
随机有限阶段的最优控制问题的DP算法与确定问题有着类似的地方:
- 利用子问题来将多阶段的优化拆分为单阶段的优化
- 对所有的$k$和$x_k$向后产生值$J_k^\star(x_k)$,给出了$k$阶段$x_k$状态下最优的cost-to-go
- 通过DP等式中的最小化获得一个最优策略
- 值空间近似同样适用,利用$\tilde{J}_k$近似$J_k^\star$