该节内容摘自于《Reinforcement Learning and Optimal Control》Chapter 2 Approximation in Value Space。
2.1 值空间近似问题
通过DP求解最优控制问题的精确解往往是不现实的,原因在于维数灾难(curse of dimensionality)。通常对于以DP为基础的次优控制有两种常见的方法。第一种便是值空间近似,我们利用其他函数$\tilde{J}_k$来对最优cost-to-go函数$J_k^\star$进行近似。然后我们在DP等式中用$\tilde{J}_k$替代$J_k^\star$。
\[\tilde{\mu}_k (x_k) \in \arg \min_{u_k \in U_k(x_k)} E \left \{ g_k(x_k,u_k,w_k) + \tilde{J}_{k+1}(f_k(x_k,u_k,w_k)) \right \} \tag{2.1}\]这构造了一个次优策略${\tilde{\mu}0,…,\tilde{\mu}{N-1}}$。注意到等式右端项是可以被看作一个近似Q因子的
\[\tilde{Q}_k(x_k,u_k) = E \left \{ g_k(x_k,u_k,w_k) + \tilde{J}_{k+1}(f_k(x_k,u_k,w_k)) \right \} \\ \tilde{\mu}_k(x_k) \in \arg \min_{u_k \in U_k(x_k)} \tilde{Q}_k(x_k,u_k)\]基于(2.1)的值空间近似通常被认为是单步前瞻(one-step lookahead),因为未来成本是在走了一步后利用$\tilde{J}{k+1}$进行近似的。除此外,还有多步前瞻的存在,我们最小化$l$个阶段后的未来成本近似值$\tilde{J}{k+l}$。
策略空间近似
除了值空间近似外,还有策略空间近似,我们通过在一个较为严格的策略族内进行优化。这种方法的优势在于在on-line系统操作下控制计算相较于最小化(2.1)会简单的多。然而,这种优势也可以通过将值空间近似与策略近似在两阶段方案中结合起来得到:
(1)得到近似最优cost-to-go函数$\tilde{J}_k$,通过one-step lookahead定义相应的次优策略$\tilde{\mu}_k,k=0,…,N-1$
(2)利用由$q$组$(x_k^s,u_k^s),s=1,…,q,u_k^s=\tilde{\mu}_k(x_k^s)$数据组成的训练集近似$\tilde{\mu}_k$。
Model-Based Versus Model-Free Implementation
求解过程的一个重要属性是是否运用了分析模型或是蒙特卡洛模拟来计算单步或多步前瞻中的期望值。我们分为以下两种情况:
(a)在model-based情形下,我们假定$w_k$在给定$(x_k,u_k)$的情况下的条件概率分布可以闭式表达。因此,我们可以计算任意三元组$(x_k,u_k,w_k)$的$p(w_k \vert x_k,u_k)$。在model-based计算过程中,期望值是可以通过代数运算得到的。
(b)在model-free情形下,我们利用Monte Carlo模拟来计算期望值。
2.1.1 计算值空间近似方法
关于$\tilde{J}_k$的计算,我们主要考虑四种类型的方法:
(a)Problem approximation(2.3节):利用一个简化后的优化问题的最优或是次优成本函数来作为$\tilde{J}_k$,通常这个简化后的优化问题是更易于计算的。简化的方法可能包括利用可分解结构,忽视不同类型的不确定性,减少状态空间的大小(aggregation)。
(b)On-line approximate optimization(2.4节):这类方法通常涉及次优策略或是启发式算法,在线应用来估计最优的cost-to-go值。
(c)Parametric cost approximation(第3章):此处函数$\tilde{J}_k$是从一个给定的函数参数族$\tilde{J}_k(x_k,r_k)$中获得,其中$r_k$为从某一算法中选取的参数向量。
(d)Aggregation:这是一种特别但相当严格的problem approximation形式。一个简单的例子是挑选每个阶段具有代表性的状态组成一个集合,将DP算法限制在这些状态上。
2.1.2 离线与在线方法
在值空间近似中,一个重要的考量是cost-to-go函数$\tilde{J}_{k+1}$和次优控制函数$\tilde{\mu}_k,k=0,…,N-1$是离线(在控制过程开始前,对于所有的$x_k$和$k$)还是在线(在控制过程开始后,当需要的时候,对需要的状态$x_k$计算)计算的。
通常地,对于比较难的问题,控制$\tilde{\mu}_k(x_k)$是在线计算的,因为对于较大的状态空间而言存储是比较困难的。我们通过以下几点进行区分:
(1)离线方法。函数$\tilde{J}{k+1}$($\forall k$)在控制过程开始前计算。$\tilde{J}{k+1}(x_{k+1})$的值要么存储在内存中,要么通过一个简单且快速的计算得到。这样做的优点在于大部分计算都在离线状态下完成,在时刻0第一个控制应用前完成。一旦控制过程开始了,不再需要额外的计算来获得$\tilde{J}{k+1}(x{k+1})$从而完成相应的次优策略。
(2)在线方法。大部分计算是在当前状态$x_k$已知后开始执行,并且只计算与之相关的下一阶段状态$x_{k+1}$的值$\tilde{J}k(x{k+1})$。
典型的离线方案是神经网络和其他的参数式近似,而典型的在线方案是rollout和模型预测控制(model predictive control)。
2.1.3 Model-Based Simplification of the Lookahead Minimization
在单步前瞻中,在cost-to-go的近似函数$\tilde{J}_{k+1}$已知后,我们通过最小化以下表达式来计算在状态$x_k$下的次优控制$\tilde{\mu}_k(x_k)$:
\[E \left \{ g_k(x_k,u_k,w_k) + \tilde{J}_{k+1}(f_k(x_k,u_k,w_k))\right \} \tag{2.2}\]而在model-based情形下,我们可以采取一些方式来对这个过程进行简化。假定我们目前已经构造了一个数学模型,$g_k$和$f_k$都能够得到闭式表达式,$w_k$的条件概率分布也已知。那么该类问题的重点就在于如何计算期望值,并在(2.2)的基础上进行最小化。
一种在表达式中消除期望值的方法叫做certainty equivalence。在这个方法中,我们将$w_k$选择为一个典型值$\tilde{w}_k$,然后利用解决确定性问题的方案来确定控制$\tilde{\mu}_k(x_k)$
\[\min_{u_k \in U_k(x_k)} \left [ g_k(x_k,u_k,\tilde{w}_k) + \tilde{J}_{k+1}(f_k(x_k,u_k,\tilde{w}_k))\right ] \tag{2.3}\]现在再来关注最小化这一步。如果$U_k(x_k)$是一个有限集,那么可以通过brute force来完成最小化,利用大量的计算和相对成本表达式的比较。虽然这个过程会特别繁琐,但是这是可以通过平行计算来减小工作量的。而对于一些离散控制问题,整数规划的方法也可以应用其中。在一些多步前瞻的确定性问题中,我们可以使用严格精确或近似的最短路方法,比如label correcting法、$A^\star$法等。而当$U_k(x_k)$是无限集时,可以离散化为一个有限集。更高效的方法可能是利用连续空间的非线性规划技术。
对于随机问题和多步前瞻、连续控制空间,随机规划是一个不错的选择。
2.1.4 Model-Free Q-Factor Approximation in Value Space
在本节中,我们总结了一些对于随机问题从model-based过渡到model-free 策略的高阶思想。特别地,我们假定:
(a)对于任意给定的状态$x_k$和控制$u_k$,我们都可以利用仿真模拟到下一个状态$x_{k+1}$的样本概率变化,并产生相应的变化成本
(b)已知成本函数近似$\tilde{J}_{k+1}$
我们想要利用函数$\tilde{J}_{k+1}$和仿真来计算或是近似所有控制$u_k\in U_k(x_k)$的Q因子,从而选出最小Q因子和对应的单步前瞻控制
\[E \left \{ g_k(x_k,u_k,w_k) + \tilde{J}_{k+1}(f_k(x_k,u_k,w_k)) \right \} \tag{2.4}\]给定状态$x_k$,我们利用仿真计算每对$(x_k,u_k)$的Q因子,然后选择最优控制。为了处理耗时的问题,我们可以引入Q因子函数的一个参数族/近似结构$\tilde{Q}_k(x_k,u_k,r_k)$,$r_k$是参数向量,利用最小二乘法/回归来近似期望值。在这里也可以扩展到利用神经网络参数结构来拟合Q因子函数。
2.1.5 Approximation in Policy Space on Top of Approximation in Value Space
在策略空间中常用的一种近似方法是引入一个策略$\tilde{\mu}_k(x_k,r_k)$的参数族,$r_k$为参数向量。参数化可能涉及到神经网络。一个通用的策略空间中参数化估计方案是获得大量的状态-控制样本$(x_k^s,u_k^s),s=1,…,q$,使得对于每个$s$,$u_k^s$对于$x_k^s$而言都是一个不错的控制。我们可以通过最小二乘回归问题来选择参数$r_k$
\(\min_{r_k} \sum_{s=1}^q \left \vert \vert u_k^s-\tilde{\mu}_k(x_k^s,r_k)\right \vert \vert^2 \tag{2.8}\) 2.1.6 When is Approximation in Value Space Effective
一个重要的问题是什么在单步前瞻方案中构成了一个优秀的近似函数$\tilde{J}_k$。一个答案是它应该与真正的最优cost-to-go函数$J_k^\star$在任意的$k$处都尽可能接近,这能够在一定程度上保证近似方案的质量。但这既不是必要的,也不是所有的甚至大多数好的实际方案所能够满足的。
举个例子,如果近似值$\tilde{J}_k(x_k)$与最优值$J_k^\star(x_k)$相差了相同的常数,那么在值空间近似方案中得到的策略是最优的。一个对于次优策略质量更精确的预测器是Q因子近似偏差$Q_k(x_k,u)-\tilde{Q}_k(x_k,u)$随着$u$的变化而逐渐改变。
2.2 多步前瞻
前文中所提到的值空间近似方案大多为单步前瞻。而多步前瞻是一种更具有“野心”、同时实现起来也更为复杂的方案。
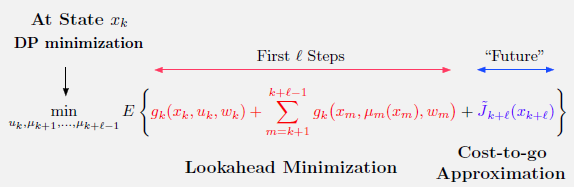
2.2.1 多步前瞻与滚动周期
与单步前瞻一样,计算$l$步前瞻的函数$\tilde{J}{k+l}$也有几种方法得到。然而,也存在另外一种可能性:当前瞻得足够远时,我们可能能够捕获到DP问题足够的特征,那么一个严格的$\tilde{J}{k+l}$选择可能就不再需要了。特别地,我们可能设置$\tilde{J}{k+l}(x{k+l}) \equiv 0$,或是$\tilde{J}{k+l}(x{k+l}) \equiv g_N(x_{k+l})$。这个思想源自于利用足够多的前瞻步数$l$,以确保对最优Q因子$Q_k$或cost-to-go函数$J_{k+l}^\star$的近似能够在一个常量范围内。这也被称为滚动周期方法,但它与简化cost-to-go函数后的多步前瞻是一样的。
当前瞻步数越来越大的时候,对一个优秀的选择$\tilde{J}_{k+l}$的需要却是逐渐消失的。原因在于在$l$步前瞻中的cost-to-go近似由两项组成:
(a)涉及前$(l-1)$阶段的一个$(l-1)$步问题的成本
(b)最终成本近似$\tilde{J}_{k+l}$
其中(a)项是可以通过精确优化得到的,那么总的近似效果只与(b)项相关,
2.2.2 多步前瞻与确定问题
在随机问题上的多步前瞻的实施总是十分耗时,因为在每一步上,我们都需要求解一定步长内的随机DP问题。然而,当问题变为确定性时,前瞻问题也是确定的,对于有限空间问题可以利用最短路方法进行解决,对于无限空间问题可以进行离散化处理。
多步预测的部分确定形式
当问题为随机问题时,考虑部分确定的方法:在状态$x_k$,在当前阶段接受随机扰动$w_k$,但是将未来扰动$w_{k+1},…,w_{k+l-1}$固定为一些特殊值。这让我们能够在计算除第一阶段外的近似cost-to-go时采用确定性方法。特别地,在这个方法下,所需要的值$\tilde{J}{k+1}(x{k+1})$能够通过一个$l-1$步确定性最短路问题得到。然后,再将$\tilde{J}{k+1}(x{k+1})$运用于计算近似Q因子
\[\tilde{Q}_k(x_k,u_k) = E \left \{ g_k(x_k,u_k,w_k) + \tilde{J}_{k+1}(f_k(x_k,u_k,w_k)) \right \} \\ \tilde{\mu}_k(x_k) \in \arg \min_{u_k \in U_k(x_k)} \tilde{Q}_k(x_k,u_k )\]2.3 问题近似
在本节中,我们主要考虑两种方法:
(1)通过可分解结构简化问题,比如将耦合约束替换为更简单的解耦约束或拉格朗日乘子相关的惩罚
(2)简化问题的概率结构,如将随机扰动替换为确定扰动
另一个也可以被视为问题近似的方法是聚合(aggregation),我们将原始问题近似为一个维度更少的问题。
2.3.1 Enforced Decomposition
简化/近似方法往往适用于在系统等式/成本函数/控制约束中包含了一堆耦合的子系统的问题,反耦合程度需要相对较弱。我们很难去定义什么是弱耦合,但在特定的问题情境下,通常这种类型的结构是十分容易辨识的。对于这类问题,我们可以将子系统解耦,构造一个更简单的问题或一个更简单的成本计算,将子系统隔离起来处理。
单次优化单个子系统
当一个问题涉及多个子系统时,一种近似方法是单次优化单个子系统。例如在$N$阶段确定性问题中,在状态$x_k$下的控制$u_k$由$n$个分量组成,$u_k = {u_k^1,…,u_k^n}$,$u_k^i$对应第$i$个子系统。
2.4 Rollout
Rollout的目标在于策略改善(policy improvement),即从一个次优/启发式策略开始,通常称为基策略(base policy),然后通过在末端使用启发式的有限前瞻最小化来产生一个改善策略。在最基本的单步前瞻中,rollout的定义非常简单:它就是在值空间近似中通过执行基策略来计算cost-to-go近似值$\tilde{J}{k+1}(x{k+1})$。同样也存在$l$步前瞻的版本,启发式算法被用来计算cost-to-go近似值$\tilde{J}{k+l}(x{k+l})$。基策略的选择对于rollout方法来说是非常重要的。实际经验表明基策略的选择大有讲究,因为即使是很烂的基础启发式算法,有时候也能够得到非常好的rollout表现。
rollout和problem approximation间也存在着一定的联系。假定我们利用基础启发式算法作为近似问题的最优策略。那么当终端成本函数近似等于近似问题的最优成本时,单步rollout策略和单步前瞻策略是相同的。
2.4.1 On-Line Rollout for Deterministic Finite-State Problems
现在回到有限数量控制和给定初始状态的确定DP问题。在时刻$k$的状态$x_k$下,rollout考虑在所有可能状态$x_{k+1}$下开始的子问题,通过使用一些算法(如基础启发式算法)得到他们的次优解。因此,在$x_k$时,rollout在线产生下一个状态$x_{k+1}$,利用基础启发式算法计算状态序列${x_{k+1},…,x_N}$和控制序列${u_{k+1},…,u_{N-1}}$,满足$x_{i+1}=f_i(x_i,u_i),i=k,…,N-1$。
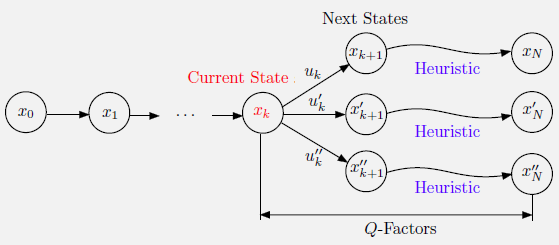
rollout算法选择最小化以下表达式的控制:
\[g_k(x_k,u_k) + g_{k+1}(x_{k+1},u_{k+1})+\cdots+g_{N-1}(x_{N-1},u_{N-1})+g_N(x_N)\]等价地,rollout在状态$x_k$下应用以下控制:
\[\tilde{\mu}_k(x_k) \in \arg \min_{u_k \in U_k(x_k)} \tilde{Q}_k(x_k,u_k)\]其中,$\tilde{Q}k(x_k,u_k)=g_k(x_k,u_k)+H{k+1}(f_k(x_k,u_k))$。$H_{k+1}(x_{k+1})$表示基础启发式算法从状态$x_{k+1}$开始的成本。
rollout算法中的成本改善 - Sequential Consistency
rollout算法的定义给我们对于基础启发算法的选择留下了空白。在次优算法中,我们通常会选用贪婪算法、局部搜索、遗传算法、禁忌搜索等等。显然,基础算法的选择主要要求在于所求解的质量和计算可行性间的平衡。
直觉地,我们希望rollout策略的表现是不会差于基础启发式算法的。由于rollout在应用启发式算法前并对第一个控制进行了优化,因此有理由推测它比在没有第一个控制优化的情况下应用启发式表现得更好。但是,为了保证这种cost-improvement性质,必须具备一些特殊条件。在此我们给出了两个这样得条件,sequential consistency和sequential improvement,然后展示了如何修改算法来处理不满足这些条件的情况。
Sequential consistent:当基础启发式算法产生从$x_k$开始的序列${x_k,…,x_N}$,它同样也产生了从$x_{k+1}$开始的序列${x_{k+1},…,x_N}$时,我们就称这个基础启发式算法是sequentially consistent的。换言之,基础启发式算法是“持续到底”的,当初始状态由$x_k$沿状态路径移动到$x_{k+1}$,基础启发式算法不会偏离剩下的路径。从起点出发,通过启发式算法设定好路线,沿着路线到达下一个点后,再次通过启发式算法设定路线,这个路线和在起点设定的路线是一致的。
从概念上讲,sequential consistency其实与启发式作为合法DP策略是一致的。这意味着存在一个策略${\mu_0,…,\mu_{N-1}}$,使得从任意状态$x_k$开始的基础启发式生成的序列都与由${\mu_0,…,\mu_{N-1}}$开始于状态$x_k$生成的序列是一样的。可以注意到,策略显然具有sequential consistency,并且相反,一个sequential consistent的基础启发式定义了一个策略:从$x_k$移动到路径${x_k,x_{k+1},…,x_N}$上的状态$x_{k+1}$由基础启发式算法生成。
基于这个事实,我们可以认为使用具有sequential consistency属性的启发式算法所得到的rollout算法比基本启发式算法产生了更优的解。特别地,令rollout策略表示为$\tilde{\pi}={\tilde{\mu}0,…,\tilde{\mu}{N-1}}$,$J_{k,\tilde{\pi}}(x_k)$表示用$\tilde{\pi}$获得的从$x_k$开始的成本,我们可以得到:
\[J_{k,\tilde{\pi}}(x_k) \leq \hat{J}_k(x_k), \quad for \ all \ x_k \ and \ k\]$\hat{J}k(x_k)$表示用基础启发式算法从$x_k$开始得到的成本。我们可以通过归纳法证明该式。当$k=N$时,$J{N,\tilde{\pi}}=H_N=g_N$,此时该不等式显然成立。假定当$k=k+1$(第$k+1$阶段)时同样成立。那么对于任意的状态$x_k$,$\bar{u}_k$为基础启发式算法在$x_k$处计算得到的控制,那么我们有
\(\begin{align} J_{k,\tilde{\pi}}(x_k) &= g_k(x_k,\tilde{\mu}_k(x_k)) + J_{k+1,\tilde{\pi}}\left ( f_k(x_k, \tilde{\mu}_k(x_k)) \right ) \\ & \leq g_k(x_k,\tilde{\mu}_k(x_k)) + H_{k+1}(f_k(x_k,\tilde{\mu}_k(x_k))) \\ & = \min_{u_k \in U_k(x_k)} [g_k(x_k,u_k) + H_{k+1}(f_k(x_k,u_k))] \\ & \leq g_k(x_k,\bar{\mu}_k) + H_{k+1}(f_k(x_k,\bar{u}_k)) \\ & = H_k(x_k) \end{align}\) 第一行来自于rollout策略$\tilde{\pi}$中的DP等式,第二行成立于我们的假设($k+1$阶段成立),第三行成立于rollout算法的定义。
rollout算法中的成本改善 - Sequential Improvement
接下来,我们会进一步证明在弱于sequential consistency的条件下,rollout策略的性能也并不比其基础启发式性能差。在rollout算法$\tilde{\pi}={\tilde{\mu}0,…,\tilde{\mu}{N-1}}$中,$\tilde{\mu}k(x_k) \in \arg \min{u_k \in U_k(x_k)} \tilde{Q}k(x_k,u_k)$,$\tilde{Q}_k(x_k,u_k) = g_k(x_k,u_k)+H{k+1}(f_k(x_k,u_k))$,$H_{k+1}(f_k(x_k,u_k)$表示从状态$x_{k+1}$通过基础启发式算法计算得到的成本。
Sequential Improvement:如果对于任意的$x_k$和$k$,我们有
\[\min_{u_k \in U_k(x_k)} \left [ g_k(x_k,u_k) + H_{k+1}(f_k(x_k,u_k)) \right ] \leq H_k(x_k)\]那我们就称该基础启发式是sequentially improving的。这个式子的意思也就是:Best heuristic Q-factor at $x_k$ ≤ Heuristic cost at $x_k$。
因此,从每个起始状态$x_k$开始,用sequentially improving的基本启发式得到的rollout算法至少不会比基本启发式差。注意,当启发式sequential consistent时,它也是sequentially improving的。另一方面,对于给定的基本启发式,sequentially improving条件可能不成立。因此,重要的是要知道,任何启发式都可以通过简单的修改进行sequentially improving,正如我们接下来解释的那样。
The Fortified Rollout Algorithm
rollout算法存在一种变体,能够隐性使用sequentially improving的基本启发式,所以它也具备sequential improvement性质。我们将其称之为fortified rollout算法。
Fortified rollout算法从状态$x_0$开始,逐步产生状态序列${x_0,…,x_N}$和相应的控制序列。一到达状态$x_k$,他就将trajectory $\overline{P}k={x_0,u_0,…,u{k-1},x_k}$存储下来,称为 permanent trajectory,同时他也存储了 tentative trajectory $\overline{T}k = {x_k, \bar{u}_k, \bar{x}{k+1},\bar{u}{k+1},…,\bar{u}{N-1},\bar{x}N}$和相应的成本 $C(\bar{T}_k) = g_k(x_k,\bar{u}_k)+g{k+1}(\bar{x}{k+1},\bar{u}{k+1})+…+g_{N-1}(\bar{x}{N-1},\bar{u}{N-1}) + g_N(\bar{x}_N)$。
Tentative trajectory满足$\bar{P}_k \cup \bar{T}_k$是到算法第$k$阶段为止最佳的端到端trajectory。刚开始时,$\bar{T}_0$是通过在初始状态$x_0$下用基础启发式得到的trajectory。现在的想法是在每个满足以下条件的状态$x_k$处偏离rollout算法:基本启发式生成的trajectoty的成本大于$\bar{T}_k$,因此使用$\bar{T}_k$作为替代。
特别地,一旦到达状态$x_k$,我们如上开始执行rollout算法:对于每一个$u_k \in U_k(x_k)$和下一个状态$x_{k+1}=f_k(x_k,u_k)$,我们运行从$x_{k+1}$开始的基础启发式,找到给出最优trajectory的控制$\tilde{u}_k$,表示为
\[\tilde{T}_k = \{ x_k, \tilde{u}_k, \tilde{x}_{k+1},\tilde{u}_{k+1},...,\tilde{u}_{N-1},\tilde{x}_N\}\]相应的成本为
\[C(\tilde{T}_k) = g_k(x_k, \tilde{u}_k) + g_{k+1}(\tilde{x}_{k+1},\tilde{u}_{k+1}) + ... + g_{N-1}(\tilde{x}_{N-1},\tilde{u}_{N-1}) + g_N(\tilde{x}_N)\]传统的rollout算法会选择控制$\tilde{u}k$并移动到$\tilde{x}{k+1}$,但fortified algorithm会比较$C(\bar{T}_k)$和$C(\tilde{T}_k)$,选择其中更优的那个。特别地,当$C(\bar{T}_k) \leq C(\tilde{T}_k)$时,算法将下一状态和相应的tentative trajectory设置为
\[x_{k+1} = \bar{x}_{k+1}, \quad \bar{T}_{k+1} = \{\bar{x}_{k+1}, \bar{u}_{k+1},...,\bar{u}_{N-1},\bar{x}_N\}\]同样,当$C(\bar{T}_k) > C(\tilde{T}_k)$时,将下一状态和相应tentative trajectory设置为
\[x_{k+1} = \bar{x}_{k+1}, \quad \bar{T}_{k+1} = \{\tilde{x}_{k+1},\tilde{u}_{k+1},...,\tilde{u}_{N-1},\tilde{x}_N\}\]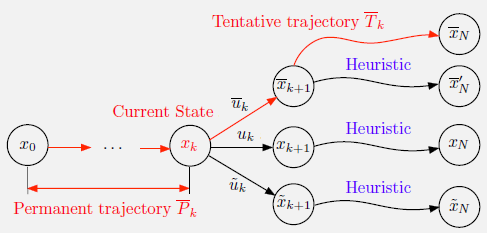
Using Multiple Heuristics
在很多问题中,几种理想的启发式算法受到青睐。那可以在rollout框架中同时使用多种启发式。这个思想便是构造一个超启发式(superheuristic),选择由所有基础启发式生成的trajectory中最好的一条。假设我们有$M$个基础启发式,然后第$m$个启发式在给定状态$x_k$的条件下生成了一条trajectory
\[\tilde{T}_{k+1}^m = \{x_{k+1},\tilde{u}_{k+1}^m,...,\tilde{u}_{N-1}^m,\tilde{x}_N^m\}\]和相应的成本$C(\tilde{T}{k+1}^m)$。然后superheuristic根据$C(\tilde{T}{k+1}^m)$的最小值产生自己的trajectory。
Rollout Algorithms with Multistep Lookahead
我们也可以在确定rollout框架中融入多步前瞻。假设我们目前位于状态$x_k$,我们对每个二步前瞻状态$x_{k+2}$运用基础启发式,并计算从$x_k$到$x_{k+1}$的两阶段成本,加上从$x_{k+2}$出发的基础启发式成本。我们选择成本最小的状态$\tilde{x}{k+2}$,然后计算从$x_k$到$x{k+2}$的控制$\tilde{u}k$和$\tilde{u}{k+1}$,选择$\tilde{u}_k$作为下一个rollout控制。

2.4.2 Stochastic Rollout and Monte Carlo Tree Search
我们接下来讨论状态数量有限的随机问题中的rollout算法。假设基础启发式为策略$\pi={\mu_0,…,\mu_{N-1}}$。我们首先注意到,在sequential consistency条件下所展示的sequentially improvement性质也同样适用于随机问题。特别地,将$J_{k,\pi}(x_k)$定义为从状态$x_k$开始基策略的相应成本,$J_{k,\tilde{\pi}}(x_k)$为从状态$x_k$开始的rollout算法的相应成本。我们可以证明:
\[J_{k, \tilde{\pi}}(x_k) \leq J_{k,\pi}(x_k), \quad for \ all \ x_k \ and \ k\]证明方法与确定问题类似。显然当$k=N$时,$J_{N,\tilde{\pi}}=J_{N,\pi}=g_N$。假定索引为$k+1$时同样成立。那么对于所有的$x_k$,有
\[\begin{align} J_{k,\tilde{\pi}}(x_k) &= E \left \{ g_k(x_k,\tilde{\mu}_k(x_k),w_k)+J_{k+1,\tilde{\pi}}(f_k(x_k,\tilde{\mu}_k(x_k),w_k))\right \} \\ & \leq E \left \{ g_k(x_k,\tilde{\mu}_k(x_k),w_k)+ J_{k+1,\pi}(f_k(x_k,\tilde{\mu}_k(x_k),w_k))\right \} \\ & = \min_{u_k\in U_k(x_k)} E \left \{ g_k(x_k,u_k,w_k) + J_{k+1,\pi}(f_{k}(x_k,u_k,w_k))\right \} \\ & \leq E\left \{ g_k(x_k, \mu_k(x_k),w_k) + J_{k+1,\pi}(f_{k}(x_k,u_k,w_k))\right \} \\ & = J_{k,\pi}(x_k) \end{align}\]Simulation-Based Implementation of the Rollout Algorithm
一个直接计算某状态$x_k$下的rollout控制的方式时直接考虑每一个可能的控制$u_k \in U_k(x_k)$,然后从$(x_k,u_k)$产生很多数量的模拟trajectories。因此,一条模拟trajectory具有以下形式
\[x_{i+1} = f_i(x_i,\mu_i(x_i), w_i), \quad i=k+1,...,N-1\]${\mu_{k+1},…\mu_{N-1}}$是基础策略的一部分,第一个生成的状态为$x_{k+1}=f_k(x_k,u_k,w_k)$,扰动序列${w_k,…,w_{N-1}}$为独立随机样本。对应$(x_k,u_k)$的trajectories的成本可以被看作是Q因子的样本
\[Q_k(x_k,u_k) = E \left \{ g_k(x_k,u_k,w_k) + J_{k+1,\tilde{\pi}}(f_k(x_k,u_k,w_k)) \right \}\]其中$J_{k+1,\tilde{\pi}}$是基础策略的cost-to-go函数。对于具有很多阶段的问题,通常还会截断rollout trajectories,并添加terminal cost function近似来补偿由此产生的误差。
通过Monte Carlo平均样本trajectories的成本,再加上terminal cost,我们就得到了每个控制$u_k \in U_k(x_k)$的Q因子$Q_k(x_k,u_k)$的近似值,表示为$\tilde{Q}_k(x_k,u_k)$。然后我们计算近似rollout控制
\[\tilde{\mu}_k(x_k) \in \arg \min_{u_k \in U_k(x_k)} \tilde{Q}_k(x_k,u_k)\]Monte Carlo Tree Search
在rollout算法的执行过程中,我们隐式地假定一旦我们到达状态$x_k$,我们就产生相同足够大数量的从$(x_k,u_k)$出发的trajectories。但这样做存在着许多缺点:
(a)由于阶段长度$N$过大,trajectories可能是非常长的
(b)一些控制$u_k$可能明显劣于其他控制,可能并不值得抽样
(c)一些控制$u_k$看上去十分优秀,可能值得通过多步前瞻进一步探索
这三个问题催生出了Monte Carlo tree search(MCTS),旨在在计算时间与性能之间取舍平衡。特别地,对于(a)的一个简单补救措施是我们只在一个限制的长度范围内使用rollout算法,而对于后续未考虑的长度,我们通过一个terminal cost approximation来表示。terminal cost函数可能比较简单或者能够通过一些辅助计算获得。事实上用在rollout中的基础策略可能正是能提供terminal cost function approximation的那一个。
一个较为简单但并没有那么直接的对(b)的补救是利用一些启发式或者统计试验来丢掉一些控制$u_k$。类似地,对于(c),我们可以用一些启发式来选择性地对某些控制$u_k$增长前瞻步数。
2.5 On-Line Rollout for Deterministic Infinite-Spaces Problems - Optimization Heuristics
我们到目前为止看到了许多在离散空间中rollout的应用,在每个状态$x_k$的相关Q因子能够通过仿真进行评估并相互比较。而在连续空间环境中,控制约束首先必须得是离散化的,而这给我们的问题带来了不便。在本节中,我们给出了另一种可选的方法,用于解决无限数量控制和$x_k$的Q因子的确定性问题,而不必依赖离散化。思想便是使用一个涉及连续优化的基础启发式,并依赖于非线性规划方法来解决相应的前瞻优化问题。
考虑单步前瞻rollout最小化
\[\tilde{\mu}_k(x_k) \in \arg \min_{u_k \in u_k(x_k)} \tilde{Q}_k(x_k,u_k)\]其中,$\tilde{Q}k(x_k,u_k)$为近似Q因子,$\tilde{Q}_k(x_k,u_k)=g_k(x_k,u_k)+H{k+1}(f_k(x_k,u_k))$。假设我们现在有一个对于$H_{k+1}$的可微闭式表达式,函数$g_k$和$f_k$都是已知且相对$u_k$可微的。那么近似Q因子$\tilde{Q}k(x_k,u_k)$也是关于$u_k$可微的,而它的最小化是可以由很多梯度相关的方法实现的。但这个方法需要我们能够得到启发式成本$H{k+1}(x_{k+1})$的闭式表达式,这是一个非常严格的要求。然而,这个困难是可以通过使用本身基于多步优化的基础启发式来避免的。特别地,假定$H_{k+1}(x_{k+1})$是一些$(l-1)$阶段的确定性最优控制问题的最优成本(与原问题相关)。然后,通过求解$l$阶段确定性最优控制问题,将基于$u_k$的第一阶段最小化与基础启发式的$(l-1)$阶段最小化无缝衔接起来,实现rollout算法。
2.5.1 Model Predictive Control
我们考虑一个经典的控制问题,其目标是使确定性系统的状态接近状态空间的原点或接近给定的轨迹。Model predictive control(MPC)正诞生于这个问题。它将我们前面提到的概念融合在了一起:多步前瞻,无限控制空间的rollout和certainty equivalence。除了在$x_k$处解决无限多Q因子的难题,同时充分处理状态和控制约束,MPC非常适合于在线重新规划,就像所有rollout算法一样。
我们目前主要关注MPC的最常见形式,其中系统要么是确定性的,要么是随机的,但它被一个确定性版本所替代,通过使用典型值来代替不确定量,类似于certainty equivalent控制方法。而且,我们所考虑的目标为使状态尽可能接近原点,我们将其称为regulation problem。
考虑一个确定性系统
\[x_{k+1}=f_k(x_k,u_k)\]其中状态$x_k$和控制$u_k$都是由有限标量元素组成的向量。每阶段的成本假定为非负的
\[g_k(x_k,u_k) \geq 0, \quad for \ all \ (x_k,u_k)\]并且存在状态和控制约束
\[x_k \in X_k, \quad u_k \in U_k(x_k), \quad k=0,1,...\]我们也假定在系统初始时刻成本为0,即
\[f_k(0,\bar{u}_k)=0,\quad g_k(0,\bar{u}_k)=0 \quad for \ some \ control \ \bar{u}_k \in U_k(0)\]对于给定的初始状态$x_0 \in X_0$,我们想要得到一个序列${u_0,u_1,…}$,使得系统的状态和控制能够在满足约束的同时将成本保持得比较小。
The MPC Algorithm
在当前状态$x_k$:
(a)MPC解决该问题的$l$步前瞻版本,但需要$x_{k+l}=0$
(b)如果${\tilde{u}k,…,\tilde{u}{k+l-1}}$是该问题的最优控制序列,MPC选择应用$\tilde{u}k$并忽略其他控制$\tilde{u}{k+1},…,\tilde{u}_{k+l-1}$
(c)在下一阶段,MPC重复这个过程
特别地,在典型阶段$k$和状态$x_k \in X_k$,MPC算法解决一个涉及相同成本函数和需求$x_{k+l}=0$的$l$阶段最优控制问题。问题如下:
\[\min_{u_i,i=k,...,k+l-1} \sum_{i=k}^{k+l-1} g_i(x_i,u_i)\]满足系统等式约束
\[x_{i+1} = f_i(x_i,u_i), \quad i=k,...,k+l-1\]状态与控制约束
\[x_i \in X_i, \quad u_i \in U_i(x_i), \quad i=k,...,k+l-1\]和终点状态约束
\[x_{k+l}=0\]假设${\tilde{u}k,…,\tilde{u}{k+l-1}}$是对应的最优控制序列,MPC在阶段$k$应用控制$\tilde{u}_k$,而不应用后续控制。为了保证存在整数$l$满足MPC算法可行,我们作出如下假设:
Constrained Controllability Condition
存在一个整数$l > 1$,使得对于每个初始状态$x_k \in X_k$,我们都可以找到一个控制序列${u_k,…,u_{k+l-1}}$,使得系统在时刻$k+l$时的状态$x_{k+l}$为0,同时满足所有中间的状态和控制约束。
一般情况下,如果控制约束不太严格,且状态约束不允许与原点有较大的偏差,那么constrained controllability condition是倾向于被满足的。注意到,MPC实际产生的状态trajectory可能永远也不能达到原点,因为我们只使用了序列${\tilde{u}k,…,\tilde{u}{k+l-1}}$中的第一个控制$\tilde{u}k$,它是在$x{k+l}=0$条件下得到的。而在下一个阶段$k+1$,我们通过MPC得到的控制是在$x_{k+l+1}=0$条件下得到的。
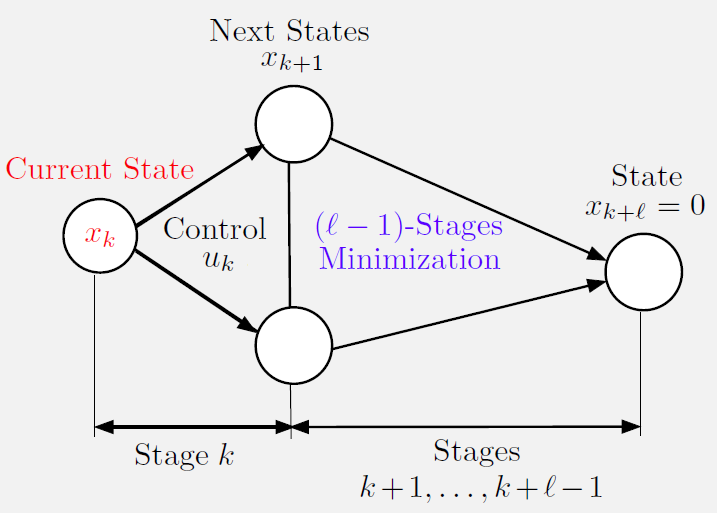
为了将rollout和MPC联系起来,我们注意到MPC所使用的一步前瞻函数$\tilde{J}$隐式是某个基本启发式的cost-to-go函数。在这个启发式中,我们在$l-1$阶段后(并非$l$阶段)将状态驱动到0,并在此后保持状态为0,同时观察状态和控制约束,并最小化相关的$l-1$阶段的成本。

