该节内容摘自于《Reinforcement Learning and Optimal Control》Chapter 3 Parametric Approximation。显然，为了在值空间中成功近似，选择一类适合手头问题的前瞻函数$\widetilde{J}_k$是非常重要的。在上一章中，我们讨论了几种基于问题近似来推出$\widetilde{J}_k$的方法。在本章中，我们将讨论另一种方法，即选择$\widetilde{J}_k$作为参数函数类（包括神经网络）的成员，其参数通过使用某种算法“优化”或“训练”。

---

3.1 近似结构

本章所提出方案的出发点便是一类函数$\widetilde{J}k(x_k, r_k)$，对于每一个k，输入当前状态$x_k$和一个由$m$个可调整的系数参数组成的向量$r_k = (r{1,k},…,r_{m,k})$（也称之为权重）。通过调整权重，我们可以利用$\widetilde{J}_k$对真实的最优的cost-to-go函数$J_k^\star$做出极佳的近似。 这一类函数$\widetilde{J}_k$便被称之为近似结构（approximation architecture），而选择参数向量$r_k$的过程称之为training或tuning。

最简单的training方法便是在参数向量空间里做一些简单的半穷举或是半随机搜索。大部分系统方法都基于数值优化，例如最小二乘拟合，旨在将近似结构产生的成本近似与训练集中的数据相拟合，即通过某种形式采样得到的大量状态价值和成本价值。

3.1.1 基于线性和非线性特征的结构

近似结构也可以分为很多类，如基于多项式、小波函数、离散化/插值方案、神经网络等等。一种比较有趣的cost approximation涉及到特征提取，将状态$x_k$映射到某个向量$\phi_k(x_k)$，称为在时刻$k$与状态$x_k$关联的特征向量。该向量由以下系数组成：

\[\phi_{1,k}(x_k),\cdots,\phi_{m,k}(x_k)\]

称之为特征。一个基于特征的cost approximation有着如下的形式：

\[\widetilde{J}_k(x_k, r_k) = \hat{J}_k(\phi_k(x_k), r_k)\]

这里的$r_k$是参数向量。因此，cost approximation的方法依赖于通过状态$x_k$提取到的特征$\phi_k(x_k)$

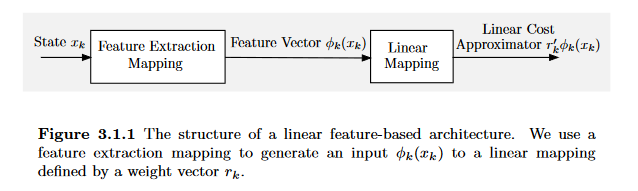
值得注意的是，在不同阶段$k$，所提取的特征$\phi_k(x_k)$和参数向量$r_k$是允许不同的。这对于nonstationary的问题（如状态空间随着时间变化）是十分有必要的。

Features通常是通过人工提取，根据人类的一些先验知识中当前状态最重要的特点。当然也存在一些系统构建特征的方式，如神经网络。

之所以使用特征的原因之一是最优的cost-to-go函数$J_k^\star$可能是一个复杂的非线性映射，所以需要将他们的复杂性进行一步步地分解。并且，如果特征能够解决$J_k^\star$中大部分的非线性，那么我们就可以使用一个相对简单的结构$\hat{J}_k$来估计$J_k^\star$，比如说关于特征的线性函数，即

\[\widetilde{J}_k(x_k, r_k) = \hat{J}_k(\phi_k(x_k), r_k) = \sum_{l=1}^m r_{l,k} \phi_{l,k}(x_k) = r_k^{'}\phi_k(x_k)\]

这被称之为基于线性特征的结构，系数参数$r_{l,k}$也被称之为权重。此类结构只需要简单的训练算法便可以完成训练。

3.1.2 线性和非线性结构的训练

选择参数向量$r$的过程便称之为训练。最常用的训练类型是基于最小二乘优化。我们将由状态-成本对$(x^s,\beta^s),s=1,…,q$组成的集合称之为训练集，而参数$r$则由解决下述问题得到：

\[\min_r \sum_{s=1}^q(\widetilde{J}(x^s, r) - \beta^s)^2\]

该训练问题的cost function往往是非凸的，所以可能存在多个局部最小值。但对于线性结构而言，cost function是二次凸的，因此训练问题存在闭式解。

\[\widetilde{J}(x, r) = r' \phi(x)\]

整个问题变成

\[\min_r \sum_{s=1}^q (r' \phi(x^s) - \beta^s)^2\]

通过对r求导，即可得到该闭式解

\[\hat{r} = \left( \sum_{s = 1}^q \phi(x^s)\phi(x^s)'\right)^{-1} \sum_{s = 1}^q \phi(x^s) \beta^s\]

但需要注意的是，上述式子的inverse可能并不存在。为了处理这种问题，一种方法是通过regularization在最小二乘中加入一个正则项，如ridge/lasso regression。

因此，线性结构的训练相较于非线性结构具有极大的优势。在非线性结构的训练中，如神经网络，往往采用的方法是特殊的梯度算法的结合，如牛顿法，这部分训练可参考机器学习内容。

3.2 神经网络

考虑到神经网络类型多种多样，本节只介绍部分能在有限时域的DP中使用的神经网络。

在阶段$k$中（为了便捷后续index中都省略$k$），考虑如下的参数结构

\[\widetilde{J}(x,v,r) = r'\phi(x,v)\]

该结构依赖于两个参数向量$v$和$r$。我们的目标就是选择合适的$v$和$r$使得$\widetilde{J}(x,v,r)$能够估计一些cost function。整个过程同样是收集大量的状态成本对$(x^s, \beta^s), s = 1,…,q$组成训练集，然后利用最小二乘法确定近似函数$\widetilde{J}(x,v,r)$。

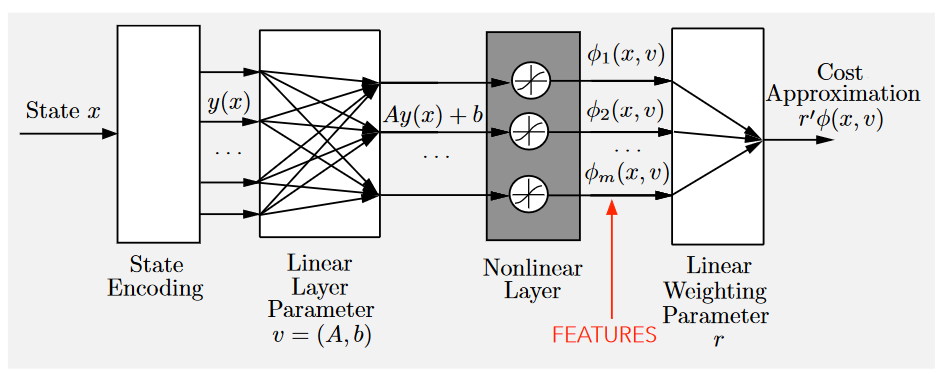
如何产生训练集与如何训练的问题稍后再讨论。可以注意到两个参数的区别，$v$更可能被视作为一个特征向量，而$r$主要作为$\phi(x,v)$的线性权重参数。

具体训练过程参考深度学习内容。

3.3 连续动态规划近似

现在介绍一种在有限时域DP问题中流行的训练近似结构$\widetilde{J}k(x_k,r_k)$的方法。参数向量$r_k$采用fitted value iteration（值迭代）算法，从DP算法的最后开始，往前推，逐个确定$r_k$：首先我们确定$r{N-1}$，然后$r_{N-2}$，以此类推。

在该算法中，对每个阶段$k$的状态空间进行采样，产生大量状态$x_k^s,s=1,…,q$。然后逐个确定参数向量$r_k$来得到一个好的最小二乘回归。

在阶段$k$，得到$r_{k+1}$后，我们通过下述问题确定$r_k$

\[r_k \in \arg \min_r \sum_{s=1}^q \left( \widetilde{J}_k(x_k^s,r) - \min_{u \in U_k(x_k^s)} E \left\{ g(x_k^s, u, w_k) + \widetilde{J}_{k+1}(f_k(x_k^s,u,w_k),r_{k+1}) \right\} \right)\]

注意这里的$x_k^s,i=1,…,q$是在第$k$阶段中抽样得到的状态（如果用全部状态，那就直接是DP，不用再做近似；在这里我们通过抽样一部分状态训练神经网络，使得神经网络能够泛化所有状态，才是主要出发点）

另一个重要的实现问题在于如何选择抽样的状态$x_k^s,i=1,…,q,k=0,…,N-1$。在实际过程中，往往是通过一些形式的蒙特卡洛仿真得到的，而他们在产生过程中是如何分布的十分重要。特别地，样本最好具有代表性，例如他们是在一个近最优的策略下经常被访问的。更准确点，样本中各种状态出现的频率应该与最优策略下它们发生的概率大致成正比，但由于最优策略难以确定，所以一般是采用一些近优策略，例如先用简单启发式对问题进行求解，收集解中的状态，抽样时就抽这些状态。

在强化学习中，数据集的生成方式被分为5种：

• Random Dataset：使用一个选择随机的固定策略生成
• Expert Dataset：训练一个在线online策略直到收敛，并使用该策略生成所有样本，无需探索
• Mixed Dataset：混合数据集是使用随机数据集（20%）和专家（Pre-Policy data）数据集（80%）的混合数据集生成的。
• Noisy Dataset：噪声数据集是由专家策略生成，且该策略选择$\epsilon-greedy(\epsilon = 0.2)$的操作
• Replay Dataset：该数据集是在线（online）策略在训练期间生成的所有样本的结合，因此由多个策略生成了数据。

3.4 Q因子参数近似

除了上述方案外，还有另一种在值空间中近似的方式。它涉及到在时刻$k$处对状态控制对$(x_k, u_k)$的最优Q因子，而无需对cost-to-go function进行中间近似。

最优Q因子定义为：

\[Q_k^*(x_k, u_k) = E \left \{ g_k(x_k,u_k,w_k) + J_{k+1}^\star(f_k(x_k, u_k, w_k)) \right \} , k = 0,...,N-1\]

此处$J_{k+1}^\star$是在阶段$k+1$最优的cost-to-go函数。因此，$Q_k^\star(x_k, u_k)$是在状态$x_k$时采用动作$u_k$所得到的成本和随后使用最优策略得到的成本之和。

因此，DP算法也可以写作：

\[J_k^\star(x_k) = \min_{u \in U_k(x_k)}Q_k^\star(x_k, u_k)\]

所以

\[Q_k^\star(x_k, u_k) = E \left \{ g_k(x_k,u_k,w_k) + \min_{u \in U_{k+1}(f_k(x_k,u_k,w_k))}Q_{k+1}^\star(f_k(x_k,u_k,w_k), u) \right \}\]

我们可以利用上式不断更新Q因子

同样地，我们也可以利用神经网络等方式对Q因子进行近似。但与此前不同的是，此前往往是对单个动作直接造成的成本进行直接计算，而对其后的状态成本进行近似。而在Q因子中，我们直接对这两个成本之和进行近似。这里的特征向量不仅依赖于状态，也依赖于所选取的动作（Q因子的输入是$x_k$和$u_k$）