本笔记为阅读《Integer Programming》中的第7章 Branch and Bound时所作。
7.1 Divide and Conquer
考虑问题:
\[Z=\max\{cx:x\in S\}\]我们需要将该问题分解为一系列更容易求解的小问题。
Proposition 7.1 Let $S=S_1 \cup \cdots\cup S_K$ be a decomposition of $S$ into smaller sets, and let $Z^k=\max {cx:x\in S_k}$ for $k = 1,…,K$. Then $Z = \max_{k} Z^k$
一个典型的分而治之的方式就是枚举树。
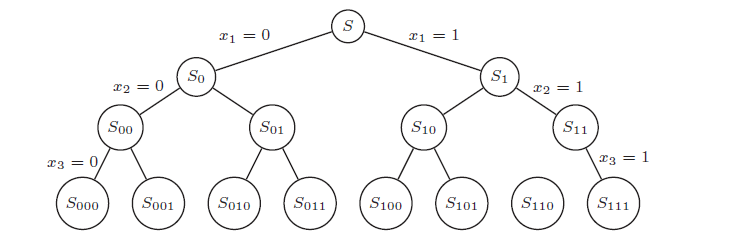
将每个问题分解为更小的、更易求解的子问题,而主问题的解从子问题的解中选取。
7.2 Implicit Enumeration
当一张图中的节点数量超过20时,完全枚举的方法对于大多数问题而言花费的时间难以忍耐。因此,我们需要将问题分解得更为巧妙。
Proposition 7.2 Let $S = S_1 \cup\cdots \cup S_K$ be a decomposition of $S$ into smaller sets, and let $Z^k = \max{cx:x\in S_k}$ for $k = 1,…,K$, $\overline{Z}^k$ be an upper bound on $Z^k$ and $\underline{Z}^k$ be a lower bound on $Z^k$. Then $\overline{Z} = \max_k{\overline{Z}^k}$ is an upper bound on $Z$ and $\underline{Z} = \max_k{\underline{Z}^k}$ is a lower bound on $Z$
我们利用bound信息来加速子问题的求解,减去一些枚举树中的枝:
- Pruning by optimality: $Z^t = {\max \space cx:x\in S_t}$ has been solved
- Pruning by bound: $\overline{Z}^t \leq \underline{Z}$
- Pruning by infeasibility: $S_t = \phi$
我们可以通过可行解信息来得到原始割/下界割,通过松弛或对偶解来得到对偶割/上界割
基于这种思想,构建一个隐式枚举算法看上去像是一项相当直接的任务,然后在这样的一个算法定义前存在着很多的问题需要解答:
什么样的松弛或对偶问题应该被用来提供upper bound?在一个相对较弱但易于计算的割和另一个强但计算时间过长的割间应该如何选择?
可行域如何分割成更小的区域$S = S_1 \cup\cdots \cup S_K$?除开二叉树外是否可以转化成三叉树、四叉树等等?在分割集合时我们应该使用一个固定的优先级规则,还是规则随着bound的改变而改变?
子问题应该以怎样的顺序进行检查?当存在一系列的仍未剪枝的子问题时,应该以怎样的标准选择下一个要解决的子问题?(后进先出/最优上界割优先…)
7.4 LP-Based Branch and Bound
一个简单的Branch and bound 算法流程图如下。
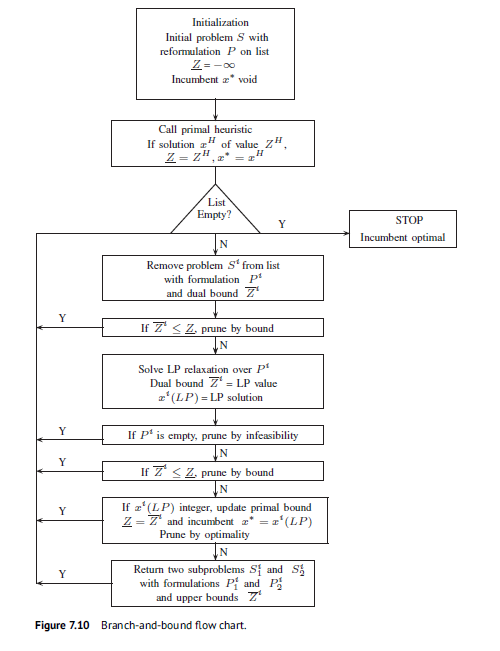
Storing the Tree
在实践中,我们并不真的将整颗枚举树存储起来,而是存储活跃节点或子问题的列表,这些活跃节点仍未被剪枝并且需要进一步探索。而此处的问题正在于多少信息应该保存下来?我们应该保存最少的信息,准备重复每一次计算,还是保存所有获得的信息?
在最少的信息情况下,我们至少需要存储已知的最优的bound和变量的上下界。通常,一个最优/近似最优基被存储用来加快线性规划松弛问题的优化。
由于问题的各异性,对于上述问题并不存在一个统一的解。所使用的规则往往基于组合优化理论、直觉和实际经验。在整数规划中,我们利用LP松弛来提供bound,利用LP解中的分数变量来进行branch。然而,通常情况下存在一个由多个候选对象组成的集合$C$的选择,我们需要一个规则来在它们间进行选择。一个常见的、并不是很有效的规则是 the most fractional variable:
\[\arg \max_{j\in C} \min[f_j,1-f_j]\]此处$f_j = x_j^{\star}-\left \lfloor x_j^{\star} \right \rfloor$,因此一个变量的分数值为$f_j = \frac{1}{2}$时是最优的。
Choosing a node
- 当我们求解得到一个原始可行解时,才有可能对树进行剪枝,得到一个理想的下界。因此,在枚举树中,我们应该尽快地下沉来找到第一个可行解。这种思想建议使用深度优先搜索策略。这种策略的另一个优点在于当一个简单约束加入原问题时,求解线性规划松弛问题非常简单。因此,鼓励从一个节点直接传递到它的一个直接子节点。
- 为了减少树中总的需要评估的节点数量,最优策略往往是选择带有最大上界的活跃节点(选择节点$s$满足$\overline{Z}_s = \max_t \overline{Z}_t$。在这样一个规则下,我们永远不会划分上界$\overline{Z}_t$小于最优值$Z$的节点。这就是最优节点优先策略。
7.5 Using a Branch-and-Bound/Cut System
为了从简单的基于LP的branch and bound算法发展到令人印象深刻的branch and cut算法,我们将会在下面引入一些重要的思想和可选项。三个最重要的思想为:
- 预处理能够提前收紧模型,减少它的大小
- 在算法过程中,通过割平面来改进公式,提供更好的对偶界
- 原始启发式算法寻找好的原始可行解并提供更好的原始界
一些其他重要的选项包括:
- 线性规划算法的选择:原始或对偶单纯形法,内点法
- 单纯形算法中进出基策略的选择
- 分支的选择和节点的选择策略:强分支、伪成本
- 特殊的建模函数:特殊的有续集和半连续变量
- 降低成本固定
- 整数变量间和分支方向间用户选择的优先级
- 对称破裂
Simplex Strategies
尽管线性规划算法经过了精心调整,但默认策略并不适合所有类型的问题。
不同的simplex pricing策略可能会在运行时间上产生巨大的影响。因此,如果重复求解类似的模型,或者线性规划看起来非常缓慢时,可以对定价策略进行一些试验。在非常大的模型中,利用内点法来求解第一个线性规划的解会是一个不错的选择。
Branching and Node Selection
假设当前问题为最大化优化问题。为了在节点列表中选取一个节点,一个自然的想法是尝试估计某个分支能够得到的最优值。
对于一个整数变量 $x_j$ ,它在LP松弛中的值为 $x_j^{\star}$,下分数为$f_j = x_j^{\star}-\left \lfloor x_j^{\star} \right \rfloor$,上分数为 $1-f_j$。定义$P_j^-,P_j^+$为伪成本,将 $x_j$ 分别减少或增加一个单位的成本估计为整数。因此,$x_j \rightarrow \lfloor x_j^{\star} \rfloor$的估计成本为 $D_j^-=f_jP_j^-$,$x_j \rightarrow \lceil x_j^{\star} \rceil$的估计成本为 $D_j^+ = (1-f_j)P_j^+$。
如果$Z_{LP}$为某节点处LP解的值,则一个对该节点值的估计为$Z_{LP}-\sum_j \min[D_j^-,D_j^+]$。我们可以通过这个估计值来选择接下来要处理的节点,最大化问题中最优节点选取策略选取值最大的节点。
而问题在于如何获取伪成本$P_j^-,P_j^+$。令$Z_j^-$为解决$x_j=\lfloor x_j^* \rfloor$时的LP问题的成本,$Z_j^+$为解决$x_j=\lceil x_j^* \rceil$时的LP问题的成本。那么,一个自然的估计便是:
\[P_j^-=\frac{Z_{LP}-Z_j^-}{f_j},\space P_j^+=\frac{Z_{LP}-Z_j^+}{1-f_j}\]然而,求解这样的估计值是十分耗时的,同样的伪成本值可能会在一棵树中的不同节点上使用,甚至$Z_j^-,Z_j^+$可能只通过一些对偶单纯变换估计得到。
这些值同样可以用来选择需要进行分支的变量。两个可能选择变量的标准是$\hat{j}=\arg \max_j{D_j^-+D_j^+}$ 或 $\hat{j}=\arg \max_j{\min(D_j^-+D_j^+)}$
Strong Branching
Strong Branching背后的思想是:在处理困难问题时,做更多的工作去尝试选择一个更优的分支变量是值得的。在LP解中,存在一个集合$C$包含值为分数的基变量,轮流在它们每一个上进行分支,在每个分支上再优化。
对于每个变量$j \in C$,在它的两个子分支中,down-branch可以得到上界$Z_j^D$,up-branch可以得到上界$Z_j^U$。那么能得到的最紧的bound的变量为:
\[j^* = \arg \min_{j \in C} \max\{Z_j^D,Z_j^U\}\]按照该规则进行分支变量的选取。明显地,求解C中每个变量的两个LP问题是十分耗时的。
Special Ordered Sets
一个type 1的特殊序列集(SOS1)是一组变量$x_1,…,x_k$中至多一个变量为正的集合。考虑特殊的SOS1情况,也称为generalized upper bound(GUB)约束,$x \in {0,1}^n$。则这个集合可以表示为:
\[\sum_{j=1}^kx_j = 1\]$x_j \in {0,1}$ for $j=1,…,k$。如果线性规划解$x^\star$中有一些变量$x_1^{\star},…,x_k^{\star}$ 为分数,则标准的分支规则为$S_1 = S \cap {x:x_j = 0},S_2 = S\cap {x:x_j=1},for \space some \space j \in {1,\cdots,k}$。然而,由于SOS1约束,${x:x_j = 0}$中只存在$k-1$种可能性${x:x_i=1}_{i \neq j}$,而${x:x_j=1}$只存在一种可能性。因此$S_1$明显要比$S_2$大得多,树是不平衡的。
SOS1分支被设计用来提供一个更为均衡的将$S$分割为$S_1$和$S_2$的方式。具体来讲,用户指定SOS1集$j_1,\cdots,j_k$的变量顺序,分支方案设置为:
\[\begin{align} S_1 &= S \cap \{x:x_{j_i}=0 \space i = 1,\cdots,r \} \space and \\ S_2 &= S\cap \{x:x_{j_i}=0 \space i = r+1,\cdots,k \} \space \end{align}\]此处$r=\min{t:\sum_{i=1}^t x_{j_i}^{*} \geq \frac{1}{2}}$。在很多情形下,SOS1约束得到的分支方案比标准方案更有效,也能够大量减少树中节点数量。
SOS2为形式为${\lambda \in R_+^k:\sum_{i=1}^k\lambda_i=1}$的集合,至多有两个变量可以为非零数,并且这两个变量一定相邻:$x_j,x_{j+1}$。
Semicontinuous Variables
若 $x=0$或$l\leq x\leq u,l\geq 0$,则可以被建模为一个semicontinuous变量 $sc(x,l,u)$。在树中的一些阶段,$x$的下界可以收缩为$l’\gt 0$,semi-continuous变量可以替换为一个正常变量$max[l,l’]\leq x\leq u$。另一方面,如果$x$的上界变为$u’\lt l$,则可以设置$x=0$
Indicator Variables
假设当一些逻辑条件满足时,约束$ax\leq b$活跃,这类逻辑条件用indicator variable表示为$z \in {0,1}$。
Priorities
优先级允许用户告知系统整数变量的相对重要性。
7.6 Preprocessing or Presolve
在解决线性规划或整数规划前,通常需要检查一下规划是否合理。所有商业的branch and cut方法都会进行检查,称为 “Preprocessing” 或 “Presolve”。基本思想是尝试快速探测和消减多余的约束和变量,尽可能缩紧bound。bound缩紧后,问题的求解也变得更快。
1. Linear Programming Preprocessing
考虑线性规划:
\[\begin{align} \max \space &2x_1+x_2-x_3 \\ &5x_1-2x_2+8x_3 \leq 15 \\ &8x_1+3x_2-x_3 \geq 9 \\ &x_1 + x_2 + x_3 \leq 6 \\ & 0 \leq x_1 \leq 3 \\ & 0 \leq x_2 \leq 1 \\ & 1 \leq x_3 \end{align}\]- Tightening Bounds
将约束1中的$x_1$独立出来,有$5x_1 \leq 15+2x_2-8x_3 \leq 15+2-8=9$,因此$x_1 \leq \frac{9}{5}$。同理,独立约束1中的$x_2,x_3$,有$x_3\leq \frac{17}{8},x_2 \geq 0$。再转到约束2,仍然采取同样的方式,得到$x_1 \geq \frac{7}{8}$。再将该式代入约束1中,得到$x_3 \leq \frac{101}{64}$
- Redundant Constraints
利用上述得到的每个变量的bound,可以发现$x_1+x_2+x_3 \lt6$,因此约束3可以被删除。现在的问题变为:
\(\begin{align} \max \space &2x_1+x_2-x_3 \\ &5x_1-2x_2+8x_3 \leq 15 \\ &8x_1+3x_2-x_3 \geq 9 \\ &\frac{7}{8}\leq x_1 \leq \frac{9}{5} \\ &0\leq x_2 \leq 1 \\ &1 \leq x_3 \leq \frac{101}{64} \end{align}\)
- Variable Fixing
考虑变量$x_2$,观察到当增加它的值时可以让约束变得更松。因为该变量在目标函数中的系数为正,那么应该把该变量放的尽可能的大,将$x_2$的值设为它的上界。另一种推出类似结论的方法是写出对偶规划。同样情况的还有$x_3$。
Proposition 7.5 Consider the set $S = {x:a_0x_0 + \sum_{j=1}^na_jx_j \leq b,l_j \leq x_j \leq k_j \space for \space j = 0,1,…,n}$.
\[x_0 \leq \left ( b - \sum_{j\geq 1:a_j \gt 0}a_jl_j - \sum_{j\geq 1:a_j < 0}a_jk_j \right ) / a_0\]
- Bounds on Variables. If $a_0 \gt 0$, then
\[\sum_{j:a_j\gt 0}a_jk_j +\sum_{j:a_j\lt 0}a_jl_j \leq b\]
- Redundancy. The constraint $a_0x_0 + \sum_{j=1}^n a_jx_j \leq b$ is redundant if
\[\sum_{j:a_j\gt 0}a_jl_j +\sum_{j:a_j\lt 0}a_jk_j \leq b\]
- Infeasibility. $S = \phi$ if
- Variable Fixing. For a maximization problem in the form: $\max{cx:Ax\leq b,l\leq x \leq k}$, if $a_{ij} \geq 0$ for all $i=1,\cdots,m$ and $c_j \lt 0$, then $x_j = l_j$. Conversely, if $a_{ij} \leq 0$ for all $i=1,\cdots,m$ and $c_j \gt 0$, then $x_j = k_j$.
2. Integer Programming Preprocessing
在整数规划问题中,preprocessing有时需要更深入。显然,当$x_j \in Z^1$且bound $l_j,k_j$不是整数时,我们可以将约束收紧为:$\lceil l_j \rceil \leq x_j \leq \lfloor k_j\rfloor$。
Generating Logical Inequalities 对于0-1整数规划而言,通常可以寻找只涉及一到两个变量的简单 “logical” 或 “Boolean” 约束,然后将他们添加到问题中来修正某些变量。如约束$7x_1+3x_2-4x_3-2x_4 \leq 1$中,我们可以得到$x_1 \leq x_3$和$x_1 \leq x_4$。
Combining Pairs of Logical Inequalities
从约束$7x_1+3x_2-4x_3-2x_4 \leq 1$和$3x_1-2x_3\geq1$中,我们可以得到$x_1=x_3$
Simplifying
Proposition 7.6 Given a 0-1 knapsack set in the form $X = {x \in {0,1}^n:\sum_{j=1}^n a_jx_j \leq b}$ with $a_j \geq 0$ for all $j$,
- $X=\emptyset$ if $b \lt 0$.
- $X = {0,1}^n$ if $\sum_{j=1}^na_j \leq b$. In other words, the constraint is redundant.
- If $a_k \gt b$, then $x_k = 0$ in all feasible solutions.
- If $a_j+a_k \gt b$ with $j \neq k$, then $x_j + x_k \leq 1$ in all feasible solutions.
- If $x_j + x_k \leq 1$ and $x_j + \bar{x}_k \leq 1(x_j \leq x_k)$, then $x_j = 0$.
- If $x_j + x_k \leq 1$ and $\bar{x}_j + \bar{x}_k \leq 1(x_j + x_k \geq 1)$, then $x_j + x_k = 1$.
- If $x_j + \bar{x}_k \leq 1$ and $\bar{x}_j + \bar{x}_k \leq 1$, then $x_k = 1$
Clique Finding
构建一张有2n个节点的图,每个节点代表一个变量$x_i$或$\bar{x}_i$。当$x_i + x_j \leq 1$时,在$x_i$和$x_j$间加上一条边;当$x_i \leq x_j$时,在$x_i$和$\bar{x}_j$间加上一条边;当$x_i + x_j \geq 1$时,在$\bar{x}_i$和$\bar{x}_j$间加上一条边。
在图中找到一个最大的Clique $C=(C^+,C^-)$,使得$C^+$为对应变量$x_i$的节点,$C^-$为对应变量$\bar{x}_i$的节点。下面给出有效clique约束:
\[\sum_{i \in C^+}x_i + \sum_{j \in C^-}(1-x_j) \leq 1\]Strengthening Inequalities
Proposition 7.7 Consider a constraint $w+ax\geq b$ where $w \in R_+^1$ and $x\in Z_+^1$.
- If $a\gt b\gt 0$, the constraint can be replaced by the tighter constraint, $w+bx\geq b$
- Consider a constraint $w+ax\leq b$, where $w\leq W$ and $x\leq k \in Z^1,x\in Z^1$. If $a \gt \alpha = W+ka-b\gt 0$, the constraint can be replaced by $w + \alpha x \leq W+\alpha(k-1)$
