<读书笔记> Large Scale Optimization

2023-02-22

1. Introduction

混合整数规划的标准形式为：

\[\begin{align*} min \ & c^Tx \\ s.t. \ & Ax\leq b \\ & x \in Z^p \times R^{n-p} \end{align*} \tag{1}\]

此处$A\in R^{m \times n}$，$c\in R^n$，$b \in R^m$，$p \in {0,…,n}$。当$p=0$时，该问题为一个线性规划问题LP；当$p=n$时，我们得到一个整数线性规划问题IP；在其它情况下，该问题为混合整数规划问题MIP。

在本章中，我们着重于求解大规模的MIP问题。求解MIP的常用精确算法主要包括：

  • lagrangian relaxation
  • cutting plane
  • branch and bound
  • branch and cut
  • column generation
  • branch and price
  • Dantzig-Wolfe decomposition
  • Benders decomposition

其中，branch and bound、branch and cut是非常通用的求解框架，适用于所有的MIP问题。而Lagrangian relaxation不能保证得到最优解，但可以得到比线性松弛更紧的界限，因此常常被用来加速branch and bound 或者branch and cut。column generation和branch and price这两个框架的通用性就弱很多，column generation不能保证获得全局最优解，而将branch and bound的框架嵌到column generation中，就构成了Branch and price的框架。

LP Relaxations

如果我们将(1)中的整数约束进行松弛，那么我们就得到

\[\begin{align*} min \ &c^Tx \\ s.t. \ & Ax \leq b \\ & x \in R^n \end{align*}\tag{2}\]

这类线性规划的有效求解方法已经有很多了。如果该LP问题的最优解为整数，那么我们就成功解决了(1)。否则，就存在一些不等式将$x^\star$与$P_1=conv({x\in Z^{n-p} \times R^p \mid Ax \leq b})$分隔开。如果我们找到了这样的不等式，我们可以将这些不等式加入LP中从而加强LP约束。这种方法也叫做cutting plane或是branch and cut。

这类方法成功的关键在于如何找到优秀的切平面。

General Cutting Planes

给定整数规划$\max {c^Tx : Ax=b,x\in Z_{+}^n}$和LP最优解$x_N^{\star}=0,x_B^\star=A_B^{-1}b-A_B^{-1}A_Nx_N^\star$，此处$B \subset {1,…,n},\mid B \mid =m,N={1,…,n}\backslash B$。假设$i \in B$且$x_i^\star \notin Z$。我们可以利用以下缩写：$\bar{a}j=A{i.}^{-1} A_{. j}$，$\bar{b}=A_{i .}^{-1}b$，$f_j=f(\bar{a}_j)$，$f_0=f(\bar{b})$，此处$f(\alpha)=\alpha - \lfloor \alpha \rfloor$。

设$A_{i.}$表示矩阵$A$的第$i$行，$A_{. j}$表示矩阵A的第$j$列，因此有

\[\begin{align*} & A_Nx_N+A_Bx_B =b\\ & x_B=A_B^{-1}b -A_B^{-1}A_Nx_N \in Z\\ \end{align*}\]

我们可以得到Gomory cut

\[\sum_{j \in N}f_jx_j \geq f_0\]

Branch and bound

Branch and bound的基础思想是“分而治之”。由于大规模问题难以直接求解，我们选择将其划分为一个个的小问题逐个解决。分割（dividing/branching）是通过将可行解集分割成更小的子集来实现的。而求解则是通过限制子集中的最优解的效果而实现的，当某个子集展现出在它的空间中不可能存在最优解时，我们就将它剔除。

Branching

当处理二元变量时，最直接分割可行解集的方法便是固定其中某一个二元变量的值，比如说一个子集中$x_1=0$，另一个子集中$x_1=1$。按照这样的方式，我们可以将一个问题不断地向下分割，展开成一个树的形式，树中每一个节点为一个子问题，一个节点的子节点是该节点所代表的问题分割出的所有子问题。

Bounding

光分解问题是没有用的，我们需要避免去求解一些无意义的子问题（无法得到最优解的问题），否则这种算法只是另一种形式上的枚举法。而这种方法的实现是通过bounding做到的。对于每一个子问题，我们对该问题进行松弛，去掉或者放松约束集中的某一个使得问题难以求解的约束。在整数问题中这类约束往往是对变量的整数约束，因此最常用的松弛方法也就是线性松弛LP relaxation。

对松弛后的问题进行求解，我们便可以得到原问题（最小化问题）目标值的一个下界。

Fathoming

一个子问题可以通过以下三种方法来对它进行处理。

  1. 如果求解松弛后的子问题，得到的最优解符合子问题的所有约束（如IP问题中松驰成LP问题后最优解仍为整数解），那么该最优解也就是子问题的最优解，不必再对该子问题进行分割，将得到的该子问题的最优目标值与当前问题目标值进行比较，更新当前问题目标值$Z^\star$的下界.
  2. 如果求解松弛后的子问题，得到的最优解不是全部符合子问题的所有约束，但它的bound大于或等于$Z^\star$，那么该问题也不必再进行分割，因为松弛后问题的可行解集变得更大，而所得到的最优解仍劣于当前得到的最优解，那再进一步缩小可行解集，也一定不能得到比当前最优解更好的解.
  3. 如果求解松弛后的子问题，此时发现该松弛后的问题无可行解，那么该问题也不必再进行分割。理由同2.

除了以上三种情况外，其余子问题均需继续向下分割并且求解

Other Options with the Branch-and-Bound Technique

每一个branch-and-bound算法都由这三步组成：branching，bounding和fathoming。而主要的柔性也体现在如何改造这三步上。

Branching总是包含选择一个仍存在的子问题并将它分解成更小的子问题。在选择的策略中，常常使用的是most recently created策略（首先选择最近创造的子问题进行分解），因为在刚刚求解完前一个子问题后对它分解出的新的子问题进行求解是十分高效的。而另一个受到欢迎的策略是best bound策略（首先选择bound最优秀的子问题进行分解），原理也很简单，最优解看上去更容易出现在目前表现最好的子问题当中。除此外，还有许多其他可选的策略。

Bounding往往是求解松弛问题实现的。然而，松弛的方式多种多样，线性松弛、拉格朗日松弛等等。

Branch and cut

Branch-and-bound方法起源于1960年代末期，但在不久后就遭遇了瓶颈。对于较小的问题（100个变量）以下，branch-and-bound可以高效地求解，但当问题规模增大时求解时间则会急剧增加。这个问题直到1980年代中期，branch-and-cut方法引入后才得以解决。Branch-and-cut方法对求解含有成百上千个变量的问题是十分便捷的，这种加速源于在三个领域的巨大进步：在BIP算法中的进步，LP算法中的进步和计算机速度的进步。

（待更新）

Column generation

考虑如下的LP模型：

\[\begin{align} Z_{MP}^*: \quad min & \sum_{j \in J} c_j x_j \\ s.t. \ & \sum_{j \in J}a_jx_j = b \\ & x_j \geq 0, j \in J \end{align}\]

定义$A=[a_{ij}]{m \times n}$，$x=[x_i]_n$，$b=[b_i]_m$。假设基变量为$x{B}$，非基变量为$x_N$，且各自对应的成本系数为$c_B$和$c_N$，对应的矩阵为$B$和$N$。所以原问题可以写作：

\[\begin{align} min \ & z = c_Bx_B+c_Nx_N \\ s.t. \ & Bx_B+Nx_N=b \\ & x_B,x_N \geq 0 \end{align}\]

因此，$x_B+B^{-1}Nx_N=B^{-1}b$，此时目标函数为$z=c_Bx_B+c_Nx_N=c_BB^{-1}b-c_BB^{-1}Nx_N+c_Nx_N=c_BB^{-1}b-(c_BB^{-1}N-c_N)x_N$

。令$\bar{c}_j$为变量$x_j$在最优表第0行的系数，所以$\bar{c_j}=c_BB^{-1}a_j-c_j$，也将这个数称为判别数，其含义为对于每个非基变量，如果其从0开始增加，目标$z$的改善率。而对于最小化问题，如果存在一个非基变量的判别数仍为正，说明当前解仍非最优，需要继续出基进基。

但对于大规模问题而言，通常矩阵中的大部分列是不需要进基的，因此可以不去产生这些无用的列。而找到具有正判别数的变量$x_j$的方法为

\[\begin{align} SP: \ & min \ -\bar{c}_j \\ & where \ the \ minimization \ is \ over \ all \ j \end{align}\]

我们不再去计算每一个$\bar{c}_j$，而是直接求解上面这个问题得到。

因此，列生成算法的思路大致如下：

1.首先我们将原问题（master problem）restrict到一个规模更小（变量数比原问题少，列数更少）的restricted master problem上，然后运用单纯形法对该restricted master problem进行求解，但此时所求到的最优解只是在restricted master problem上的，而非master problem的最优解。

2.此时，我们需要通过一个subproblem去check那些未被考虑的变量中是否有使得reduced cost小于0的，如果有，就把这个变量的相关系数列加入到restricted master problem的系数矩阵中，回到第一步。

经过反复的迭代，直到subproblem中的reduced cost rate大于等于0，那么master problem就求到了最优解。

原问题如下：

\[\begin{align} MP: \quad min \ & \sum_{i=1}^nc_ix_i \\ s.t. \ & \sum_{j=1}^na_{ij}x_j=b_i, \ i=1,...,m \end{align}\]

restricted master problem如下：

\[\begin{align} RMP: \quad min \ & \sum_{i=1}^k c_ix_i \\ s.t. \ & \sum_{j=1}^k a_{ij}x_j =b_i, \ i=1,...,m \end{align}\]

相当于在restricted master problem中将$y_{k+1},…,y_m$强制限制为非基变量。

在求解完上述的RMP问题后，我们需要检查$y_{k+1},…,y_m$中是否有可以进基的列，而这需要通过非基变量的检验数$\sigma_j = c_j -c_BB^{-1}a_j$来判断，在其中找到检验数最小且为负的变量，将变量对应的那一列添加到RMP中。而检验数中的$c_BB^{-1}$有两重含义：

  • 通过求解RMP问题得到的影子价格（shadow price）
  • 通过求解RMP对偶问题得到的对偶变量（dual variable）

我们往往采用通过单纯形法求RMP对偶问题的方式来计算$c_BB^{-1}$，因为在该问题中的变量数更少。得到$c_BB^{-1}$后我们求解下述子问题来得到需要添加进RMP的列（$a_j$）。

\[\begin{align} min \ & (c_j-c_BB^{-1}a_j) \\ s.t. \ & the \ constraints \ of \ column \ a_j \end{align}\]

Branch and price

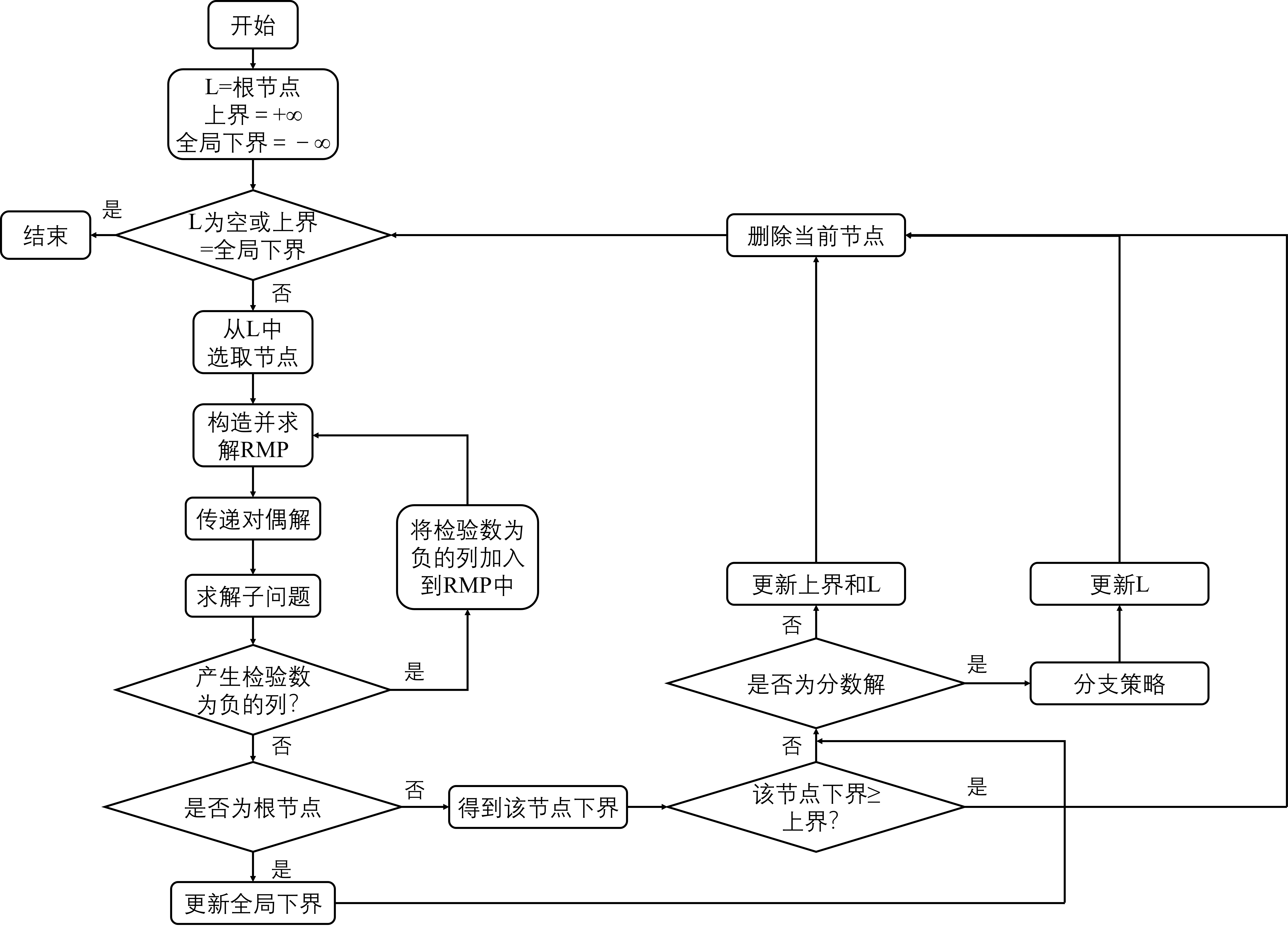
分支定价算法（Branch and price）是将分支定界与列生成结合起来的一种方法。其中，列生成算法用来求解节点的下界，即节点松弛模型的最优解。列生成算法因其求解方法的本质会大大减少计算量，求解的并非节点松弛模型本身，而是受限制的松弛模型，即减少了决策变量规模。流程图如下。

Dantzig-Wolfe decomposition

考虑如下的模型：

\[\begin{align} min \ & c^Tx \\ s.t. \ & Ax=b \\ & x \in S \end{align}\]

此处$S$为一个多面体集，代表着特殊构造的约束。假定$S$非空有界，$x_1,x_2,…,x_t$为$S$的极点，那么$\forall x\in S:x=\sum_{j=1}^t\lambda_jx_j,\ \sum_{j=1}^t \lambda_j = 1, \ \lambda_j \geq 0(j=1,…,t)$。原模型可以表示为：

\[\begin{align} MP: \quad min \ & \sum_{j=1}^t (c^Tx_j)\lambda_j \\ s.t. \ & \sum_{j=1}^t (Ax_j)\lambda_j = b \\ & \sum_{j=1}^t \lambda_j = 1 \\ & \lambda_j \geq 0(j=1,...,t) \end{align}\]

要直接枚举所有极点来解决这个问题是十分困难的。对于$MP$，假定一个基为$B$，$\lambda=[\lambda_B,\lambda_N]^T$

Benders decomposition

考虑如下的MIP模型：

\[\begin{align} \sideset{}{}{min}_{x,y}\space &cx+fy \\ s.t. \space&Ax+By=b \\ &x \geq 0 \\ &y \in Y \subset R^n \end{align}\]

其中，$c\in R^{1\times m}$，$f \in R^{1 \times n}$，$x\in R^{m \times 1}$，$y \in R^{n \times 1}$，$A \in R^{r \times m}$，$B \in R^{r \times n}$，$b \in R^{r \times 1}$。该模型中$x$是连续决策变量，而$y$是复杂决策变量，可能是0-1型决策变量，也可能是整数型决策变量。由于$y$的限制，当问题规模较大时要直接求解该MIP是非常困难的，因此我们需要一种方法来先将$y$搞定。

我们观察到，如果给定y的值，记为$\bar{y}$，那么剩余部分的模型就可以写作：

\[\begin{align} SP: \quad \sideset{}{}{min}_x \ & cx \\ s.t. \ & Ax=b-B\bar{y} \\ & x \geq 0 \end{align}\]

剩余部分的模型是线性规划模型LP，求解难度大大的降低了。求解MIP是NP-hard问题，而求解LP却是可以在多项式时间内精确求解的。该问题一般称之为子问题。

那么该如何给定$y$的值$\bar{y}$呢？我们将模型中关于$x$的部分全部去掉，可以得到以下模型：

\[\begin{align} MP_0:\quad \sideset{}{}{min}_y \space &fy \\ s.t. \space &y \in Y \subset R^n \end{align}\]

$MP_0$的求解也是十分简单的，求解得到的最优解可以作为$\bar{y}$传递给SP。该问题一般称之为主问题。但分别求解MP和SP并不能等同于求解了原MIP。因为两个问题间并非是独立的，而是存在一定关联的。要想达到等价求解MIP的目的，还需要MP和SP之间的交互。

因为MP中删除了所有关于$x$的约束，相当于抛弃了$x$的影响，但实际上$x$一定会影响MP。那我们可以尝试通过一种先试错、再补救的方法，先删除所有$x$的相关部分，构成初始的MP，然后求解SP获得一些信息，这些信息反映了$x$对$y$的影响，我们通过某种方式（割），将$x$对$y$的影响加回到MP中进行补救，求解MP中得到新的$y$代入到$SP$中。补救完成后继续求解SP，给MP加割，不断迭代，最终达到求解MIP的目的。

那么如何进行补救呢？Benders Decomposition的补救措施，是以两种割的形式加回到MP中：

  • Benders Optimality Cut
  • Benders Feasibility Cut

这两种Cut来源于SP的对偶问题：

\[\begin{align} Dual \space SP: \quad \sideset{}{}{max}_{\alpha} \space &\alpha^T(b-B\bar{y})\\ s.t. \space &A^T\alpha \leq c \\ &\alpha \space free \end{align}\]

Dual SP的可行性并不依赖于$\bar{y}$的取值

  • 如果强对偶性成立（即SP和Dual SP都有可行解），即$z_{SP}=z_{Dual SP}$

  • 根据弱对偶性，有$z_{SP}\geq z_{DualSP}$

若Dual SP的可行域为空，则要么SP对于某些$y$取值无界，要么对于所有的$y$，SP可行域也为空

。若Dual SP的可行域非空，则我们可以列出可行域的全部极点$(\alpha_p^1,…,\alpha_p^I)$和极射线$(\alpha_r^1,…,\alpha_r^J)$。（极点是可行域的几何顶点，极射线是能够保证这条射线只要起点在可行域内，沿着极射线方向移动，不管移动步长有多大，仍在可行域内）。

对于给定的$\bar{y}$，对偶问题可以通过以下方式得到解决：

  • 检查是否对于某极射线$\alpha_r^j$满足$(\alpha_r^j)^T(b-B\bar{y})>0$，若成立，则Dual SP存在大于0的解，由于$z_{SP}\geq z_{DualSP}\gt 0$，则Dual SP无界，SP不可行
  • 找到一个极点$\alpha_p^i$最大化$(\alpha_p^i)^T(b-B\bar{y})$，若成立，则SP和Dual SP都有有限最优解

因此Dual SP也可以写作：

\[\begin{align} Dual \space SP: \quad min \space &q\\ s.t. \space &(\alpha_r^j)^T(b-By) \leq 0, \forall j = 1,...,J \\ &(\alpha_p^i)^T(b-By) \leq q, \forall i = 1,...,I \\ &q \space free \end{align}\]

因此，Benders optimality cuts的具体形式为：$(\alpha_p^i)^T(b-By)\leq q,\forall i \in P$。$P$表示在迭代过程中所找到的Dual SP的极点集合，$\alpha_p^i$为Dual SP的一个极点

Benders feasibility cuts的具体形式为：$(\alpha_p^i)^T(b-By)\leq0,\forall i \in R$。$R$表示在迭代过程中所找到的Dual SP的极射线集合，$\alpha_p^i$为Dual SP的一个极射线。

Benders Decomposition 步骤

1.将原问题拆分为一个主问题MP和一个子问题SP：

\[\begin{align} MP:\space \sideset{}{}{min}_y \space &fy +q \\ s.t. \space &y \in Y \subset R^n \\ &Benders\space optimality\space cuts \\ &Benders\space feasibility\space cuts \\ &q \space free \end{align}\]

2.求解主问题，得到$y$的值$\bar{y}$并构建子问题：

  • Dual SP $\rightarrow$ 直接得到对偶变量，但需要写出SP的对偶
\[\begin{align} Dual \space SP: \quad Q(y)=\sideset{}{}{max}_{\alpha} \space &\alpha^T(b-B\bar{y})\\ s.t. \space &A^T\alpha \leq c \\ &\alpha \space free \end{align}\]
  • SP $\rightarrow$ 不用写出子问题的对偶，但需要应用CPLEX中的iIoCplex.getDuals()和iIoCplex.dualFarkas分别获取约束的对偶变量（Gurobi中对应的函数为Constr.Pi和Constr.FarkasDual）
\[\begin{align} SP: \quad Q(y)=\sideset{}{}{min}_x \space &\space cx \\ s.t. &\space Ax=b-B\bar{y} \\ &x \geq 0 \end{align}\]

3.求解子问题，获得对偶变量，构建Benders optimality cut 和 Benders feasibility cut。

  • 求解Dual SP，若存在有界可行解，构建Benders optimality cut；若无解，构建Benders feasibility cut
  • 求解SP，利用求解器得到对偶变量或者极射线

4.将步骤3构建好的cut添加到MP中，求解MP，并更新全局的上界UB和全局的下界LB。如果UB=LB，则算法停止，获得最优解。否则重复2-4步

\[\begin{align} UB &= fy + Q(y) \\ LB &= fy + q \end{align}\]

$fy+Q(y)$是给定了$y = \bar{y}$后求解SP得到$x$的值$\bar{x}$，因此$(\bar{x},\bar{y})$是原问题MIP的一个可行解，min问题的任意一个可行解一定是原问题的UB。

$fy+q$是忽略了$x$的影响，只是添加了一部分cuts，而没有把所有的cut都加回去，因此是原问题的一个松弛版本，因此可以为原问题提供一个下界